Bernhard Stankewitz
Provable Mixed-Noise Learning with Flow-Matching
Aug 25, 2025

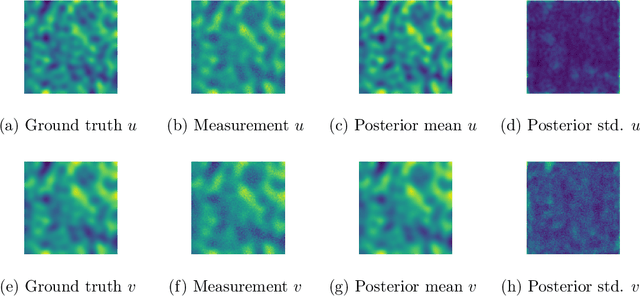
Abstract:We study Bayesian inverse problems with mixed noise, modeled as a combination of additive and multiplicative Gaussian components. While traditional inference methods often assume fixed or known noise characteristics, real-world applications, particularly in physics and chemistry, frequently involve noise with unknown and heterogeneous structure. Motivated by recent advances in flow-based generative modeling, we propose a novel inference framework based on conditional flow matching embedded within an Expectation-Maximization (EM) algorithm to jointly estimate posterior samplers and noise parameters. To enable high-dimensional inference and improve scalability, we use simulation-free ODE-based flow matching as the generative model in the E-step of the EM algorithm. We prove that, under suitable assumptions, the EM updates converge to the true noise parameters in the population limit of infinite observations. Our numerical results illustrate the effectiveness of combining EM inference with flow matching for mixed-noise Bayesian inverse problems.
EarlyStopping: Implicit Regularization for Iterative Learning Procedures in Python
Mar 20, 2025Abstract:Iterative learning procedures are ubiquitous in machine learning and modern statistics. Regularision is typically required to prevent inflating the expected loss of a procedure in later iterations via the propagation of noise inherent in the data. Significant emphasis has been placed on achieving this regularisation implicitly by stopping procedures early. The EarlyStopping-package provides a toolbox of (in-sample) sequential early stopping rules for several well-known iterative estimation procedures, such as truncated SVD, Landweber (gradient descent), conjugate gradient descent, L2-boosting and regression trees. One of the central features of the package is that the algorithms allow the specification of the true data-generating process and keep track of relevant theoretical quantities. In this paper, we detail the principles governing the implementation of the EarlyStopping-package and provide a survey of recent foundational advances in the theoretical literature. We demonstrate how to use the EarlyStopping-package to explore core features of implicit regularisation and replicate results from the literature.
Contraction rates for conjugate gradient and Lanczos approximate posteriors in Gaussian process regression
Jun 18, 2024

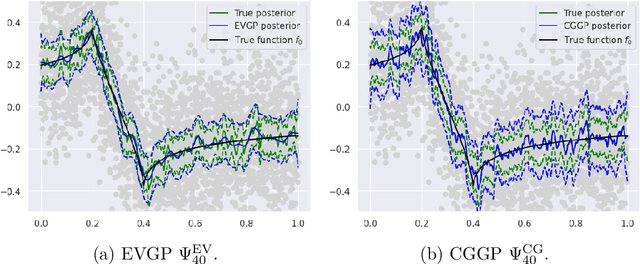

Abstract:Due to their flexibility and theoretical tractability Gaussian process (GP) regression models have become a central topic in modern statistics and machine learning. While the true posterior in these models is given explicitly, numerical evaluations depend on the inversion of the augmented kernel matrix $ K + \sigma^2 I $, which requires up to $ O(n^3) $ operations. For large sample sizes n, which are typically given in modern applications, this is computationally infeasible and necessitates the use of an approximate version of the posterior. Although such methods are widely used in practice, they typically have very limtied theoretical underpinning. In this context, we analyze a class of recently proposed approximation algorithms from the field of Probabilistic numerics. They can be interpreted in terms of Lanczos approximate eigenvectors of the kernel matrix or a conjugate gradient approximation of the posterior mean, which are particularly advantageous in truly large scale applications, as they are fundamentally only based on matrix vector multiplications amenable to the GPU acceleration of modern software frameworks. We combine result from the numerical analysis literature with state of the art concentration results for spectra of kernel matrices to obtain minimax contraction rates. Our theoretical findings are illustrated by numerical experiments.
From inexact optimization to learning via gradient concentration
Jun 24, 2021
Abstract:Optimization was recently shown to control the inductive bias in a learning process, a property referred to as implicit, or iterative regularization. The estimator obtained iteratively minimizing the training error can generalise well with no need of further penalties or constraints. In this paper, we investigate this phenomenon in the context of linear models with smooth loss functions. In particular, we investigate and propose a proof technique combining ideas from inexact optimization and probability theory, specifically gradient concentration. The proof is easy to follow and allows to obtain sharp learning bounds. More generally, it highlights a way to develop optimization results into learning guarantees.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge