Contraction rates for conjugate gradient and Lanczos approximate posteriors in Gaussian process regression
Paper and Code
Jun 18, 2024

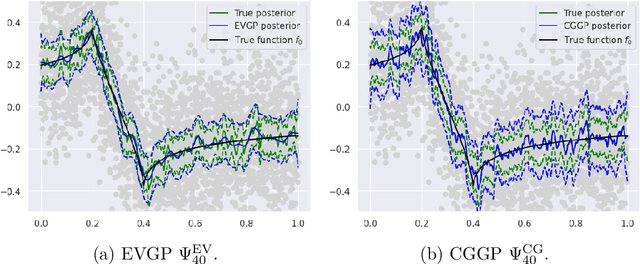

Due to their flexibility and theoretical tractability Gaussian process (GP) regression models have become a central topic in modern statistics and machine learning. While the true posterior in these models is given explicitly, numerical evaluations depend on the inversion of the augmented kernel matrix $ K + \sigma^2 I $, which requires up to $ O(n^3) $ operations. For large sample sizes n, which are typically given in modern applications, this is computationally infeasible and necessitates the use of an approximate version of the posterior. Although such methods are widely used in practice, they typically have very limtied theoretical underpinning. In this context, we analyze a class of recently proposed approximation algorithms from the field of Probabilistic numerics. They can be interpreted in terms of Lanczos approximate eigenvectors of the kernel matrix or a conjugate gradient approximation of the posterior mean, which are particularly advantageous in truly large scale applications, as they are fundamentally only based on matrix vector multiplications amenable to the GPU acceleration of modern software frameworks. We combine result from the numerical analysis literature with state of the art concentration results for spectra of kernel matrices to obtain minimax contraction rates. Our theoretical findings are illustrated by numerical experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge