Marjolein Fokkema
Hypothesis-free discovery from epidemiological data by automatic detection and local inference for tree-based nonlinearities and interactions
May 01, 2025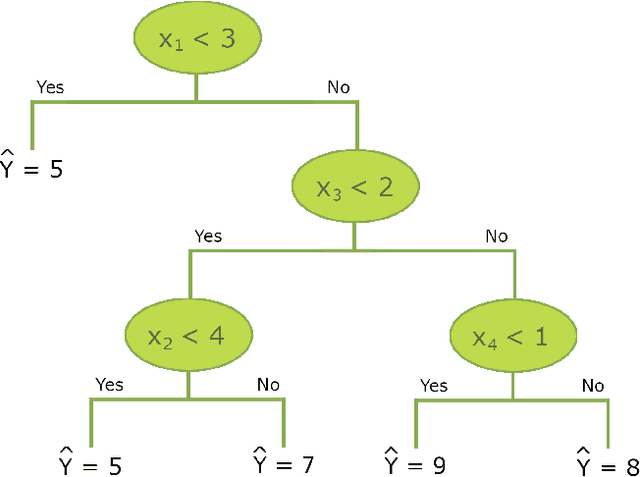

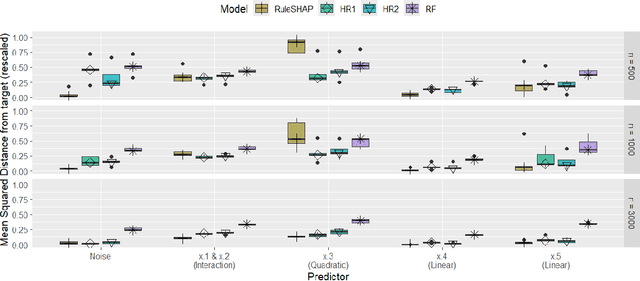
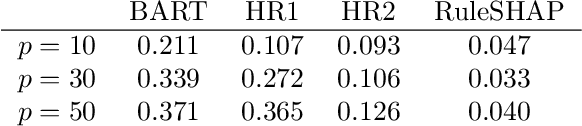
Abstract:In epidemiological settings, Machine Learning (ML) is gaining popularity for hypothesis-free discovery of risk (or protective) factors. Although ML is strong at discovering non-linearities and interactions, this power is currently compromised by a lack of reliable inference. Although local measures of feature effect can be combined with tree ensembles, uncertainty quantifications for these measures remain only partially available and oftentimes unsatisfactory. We propose RuleSHAP, a framework for using rule-based, hypothesis-free discovery that combines sparse Bayesian regression, tree ensembles and Shapley values in a one-step procedure that both detects and tests complex patterns at the individual level. To ease computation, we derive a formula that computes marginal Shapley values more efficiently for our setting. We demonstrate the validity of our framework on simulated data. To illustrate, we apply our machinery to data from an epidemiological cohort to detect and infer several effects for high cholesterol and blood pressure, such as nonlinear interaction effects between features like age, sex, ethnicity, BMI and glucose level.
Extending Explainable Ensemble Trees (E2Tree) to regression contexts
Sep 10, 2024Abstract:Ensemble methods such as random forests have transformed the landscape of supervised learning, offering highly accurate prediction through the aggregation of multiple weak learners. However, despite their effectiveness, these methods often lack transparency, impeding users' comprehension of how RF models arrive at their predictions. Explainable ensemble trees (E2Tree) is a novel methodology for explaining random forests, that provides a graphical representation of the relationship between response variables and predictors. A striking characteristic of E2Tree is that it not only accounts for the effects of predictor variables on the response but also accounts for associations between the predictor variables through the computation and use of dissimilarity measures. The E2Tree methodology was initially proposed for use in classification tasks. In this paper, we extend the methodology to encompass regression contexts. To demonstrate the explanatory power of the proposed algorithm, we illustrate its use on real-world datasets.
Subgroup detection in linear growth curve models with generalized linear mixed model (GLMM) trees
Sep 11, 2023Abstract:Growth curve models are popular tools for studying the development of a response variable within subjects over time. Heterogeneity between subjects is common in such models, and researchers are typically interested in explaining or predicting this heterogeneity. We show how generalized linear mixed effects model (GLMM) trees can be used to identify subgroups with differently shaped trajectories in linear growth curve models. Originally developed for clustered cross-sectional data, GLMM trees are extended here to longitudinal data. The resulting extended GLMM trees are directly applicable to growth curve models as an important special case. In simulated and real-world data, we assess the performance of the extensions and compare against other partitioning methods for growth curve models. Extended GLMM trees perform more accurately than the original algorithm and LongCART, and similarly accurate as structural equation model (SEM) trees. In addition, GLMM trees allow for modeling both discrete and continuous time series, are less sensitive to (mis-)specification of the random-effects structure and are much faster to compute.
Imputation of missing values in multi-view data
Oct 26, 2022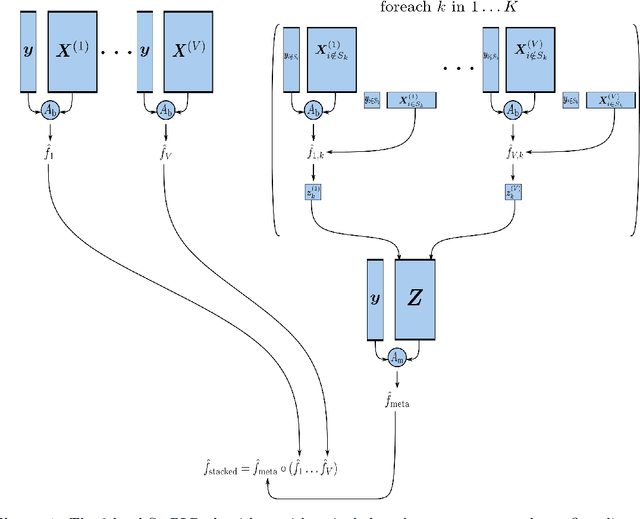
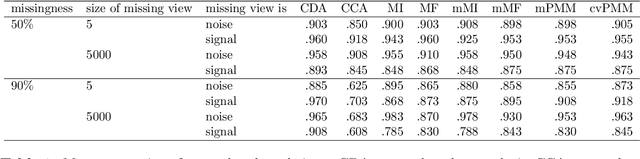
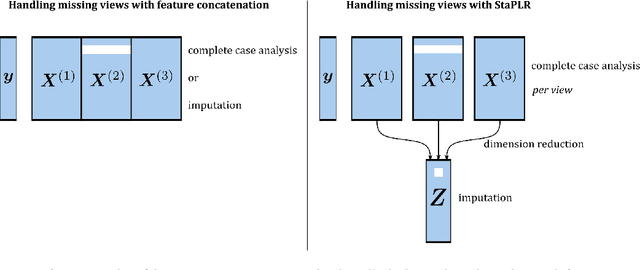
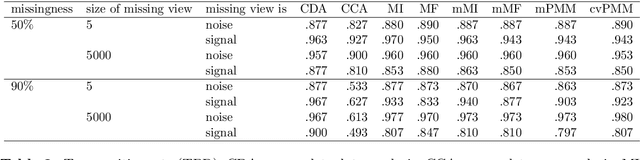
Abstract:When missing values occur in multi-view data, all features in a view are likely to be missing simultaneously. This leads to very large quantities of missing data which, especially when combined with high-dimensionality, makes the application of conditional imputation methods computationally infeasible. We introduce a new meta-learning imputation method based on stacked penalized logistic regression (StaPLR), which performs imputation in a dimension-reduced space. We evaluate the new imputation method with several imputation algorithms using simulations. The results show that meta-level imputation of missing values leads to good results at a much lower computational cost, and makes the use of advanced imputation algorithms such as missForest and predictive mean matching possible in settings where they would otherwise be computationally infeasible.
Improved prediction rule ensembling through model-based data generation
Sep 28, 2021
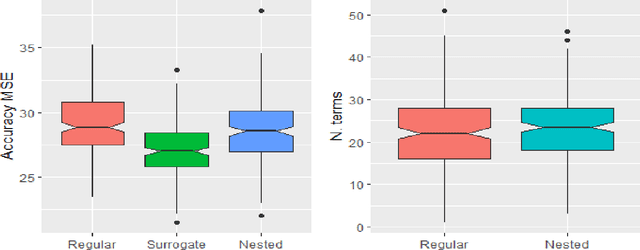

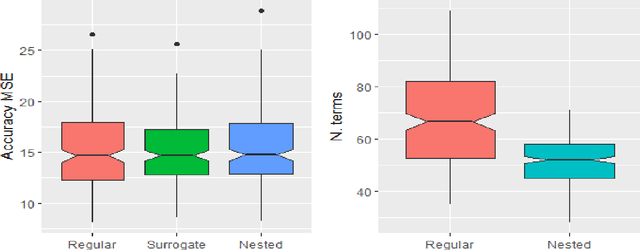
Abstract:Prediction rule ensembles (PRE) provide interpretable prediction models with relatively high accuracy.PRE obtain a large set of decision rules from a (boosted) decision tree ensemble, and achieves sparsitythrough application of Lasso-penalized regression. This article examines the use of surrogate modelsto improve performance of PRE, wherein the Lasso regression is trained with the help of a massivedataset generated by the (boosted) decision tree ensemble. This use of model-based data generationmay improve the stability and consistency of the Lasso step, thus leading to improved overallperformance. We propose two surrogacy approaches, and evaluate them on simulated and existingdatasets, in terms of sparsity and predictive accuracy. The results indicate that the use of surrogacymodels can substantially improve the sparsity of PRE, while retaining predictive accuracy, especiallythrough the use of a nested surrogacy approach.
Analyzing hierarchical multi-view MRI data with StaPLR: An application to Alzheimer's disease classification
Aug 12, 2021
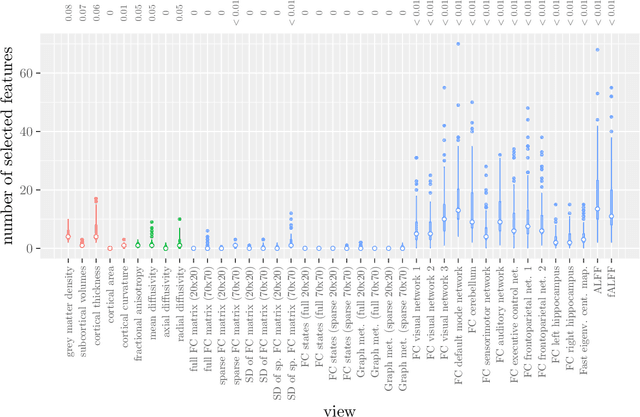
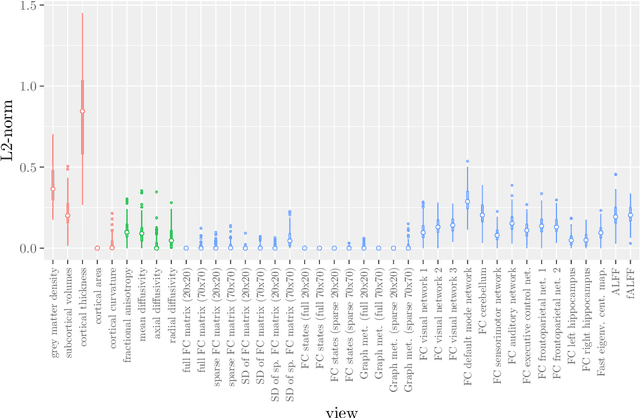
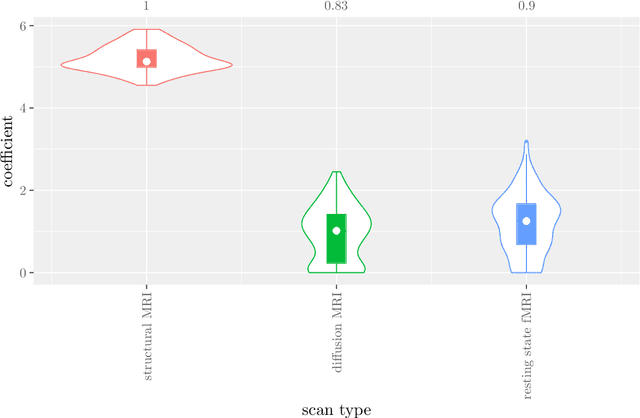
Abstract:Multi-view data refers to a setting where features are divided into feature sets, for example because they correspond to different sources. Stacked penalized logistic regression (StaPLR) is a recently introduced method that can be used for classification and automatically selecting the views that are most important for prediction. We show how this method can easily be extended to a setting where the data has a hierarchical multi-view structure. We apply StaPLR to Alzheimer's disease classification where different MRI measures have been calculated from three scan types: structural MRI, diffusion-weighted MRI, and resting-state fMRI. StaPLR can identify which scan types and which MRI measures are most important for classification, and it outperforms elastic net regression in classification performance.
View selection in multi-view stacking: Choosing the meta-learner
Oct 30, 2020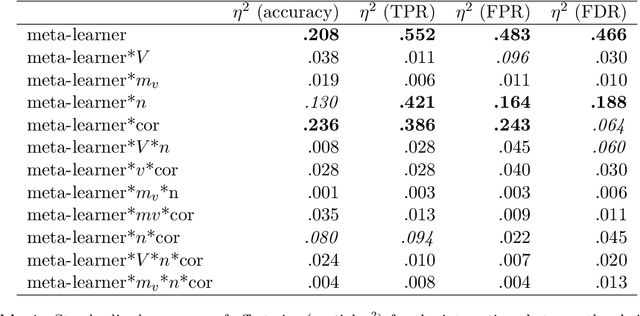
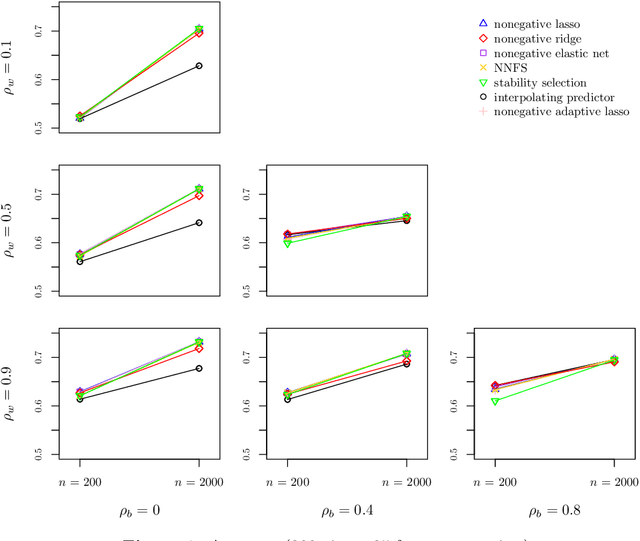
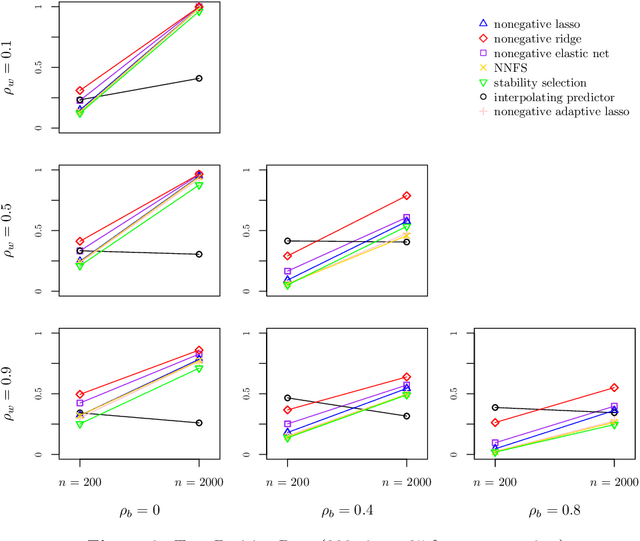

Abstract:Multi-view stacking is a framework for combining information from different views (i.e. different feature sets) describing the same set of objects. In this framework, a base-learner algorithm is trained on each view separately, and their predictions are then combined by a meta-learner algorithm. In a previous study, stacked penalized logistic regression, a special case of multi-view stacking, has been shown to be useful in identifying which views are most important for prediction. In this article we expand this research by considering seven different algorithms to use as the meta-learner, and evaluating their view selection and classification performance in simulations and two applications on real gene-expression data sets. Our results suggest that if both view selection and classification accuracy are important to the research at hand, then the nonnegative lasso, nonnegative adaptive lasso and nonnegative elastic net are suitable meta-learners. Exactly which among these three is to be preferred depends on the research context. The remaining four meta-learners, namely nonnegative ridge regression, nonnegative forward selection, stability selection and the interpolating predictor, show little advantages in order to be preferred over the other three.
Stacked Penalized Logistic Regression for Selecting Views in Multi-View Learning
Nov 06, 2018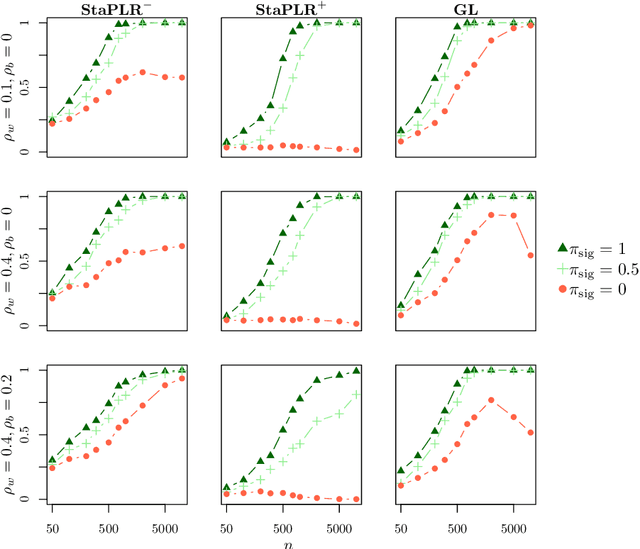
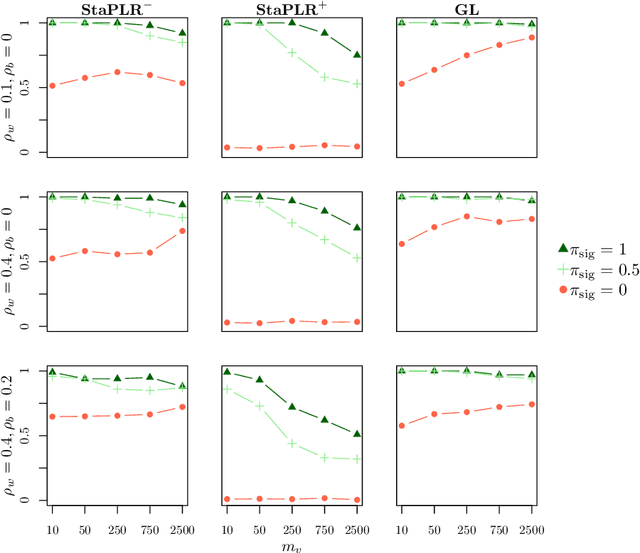
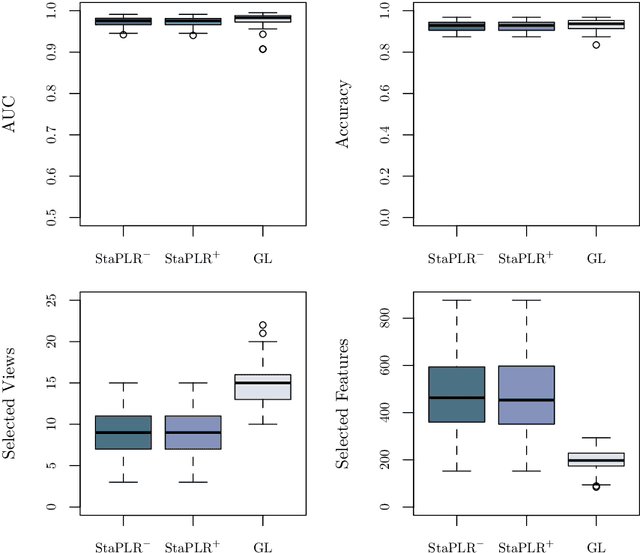
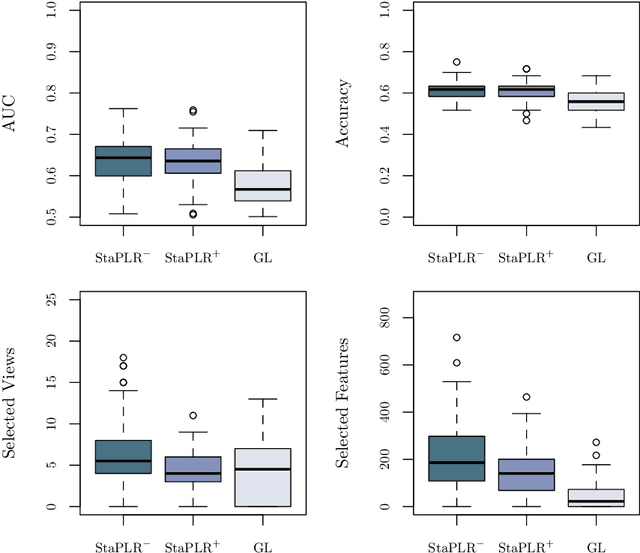
Abstract:In multi-view learning, features are organized into multiple sets called views. Multi-view stacking (MVS) is an ensemble learning framework which learns a prediction function from each view separately, and then learns a meta-function which optimally combines the view-specific predictions. In case studies, MVS has been shown to increase prediction accuracy. However, the framework can also be used for selecting a subset of important views. We propose a method for selecting views based on MVS, which we call stacked penalized logistic regression (StaPLR). Compared to existing view-selection methods like the group lasso, StaPLR can make use of faster optimization algorithms and is easily parallelized. We show that nonnegativity constraints on the parameters of the function which combines the views are important for preventing unimportant views from entering the model. We investigate the view selection and classification performance of StaPLR and the group lasso through simulations, and consider two real data examples. We observe that StaPLR is less likely to select irrelevant views, leading to models that are sparser at the view level, but which have comparable or increased predictive performance.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge