Long-term foehn reconstruction combining unsupervised and supervised learning

Foehn winds, characterized by abrupt temperature increases and wind speed changes, significantly impact regions on the leeward side of mountain ranges, e.g., by spreading wildfires. Understanding how foehn occurrences change under climate change is crucial. Unfortunately, foehn cannot be measured directly but has to be inferred from meteorological measurements employing suitable classification schemes. Hence, this approach is typically limited to specific periods for which the necessary data are available. We present a novel approach for reconstructing historical foehn occurrences using a combination of unsupervised and supervised probabilistic statistical learning methods. We utilize in-situ measurements (available for recent decades) to train an unsupervised learner (finite mixture model) for automatic foehn classification. These labeled data are then linked to reanalysis data (covering longer periods) using a supervised learner (lasso or boosting). This allows to reconstruct past foehn probabilities based solely on reanalysis data. Applying this method to ERA5 reanalysis data for six stations across Switzerland and Austria achieves accurate hourly reconstructions of north and south foehn occurrence, respectively, dating back to 1940. This paves the way for investigating how seasonal foehn patterns have evolved over the past 83 years, providing valuable insights into climate change impacts on these critical wind events.

Spatio-seasonal risk assessment of upward lightning at tall objects using meteorological reanalysis data

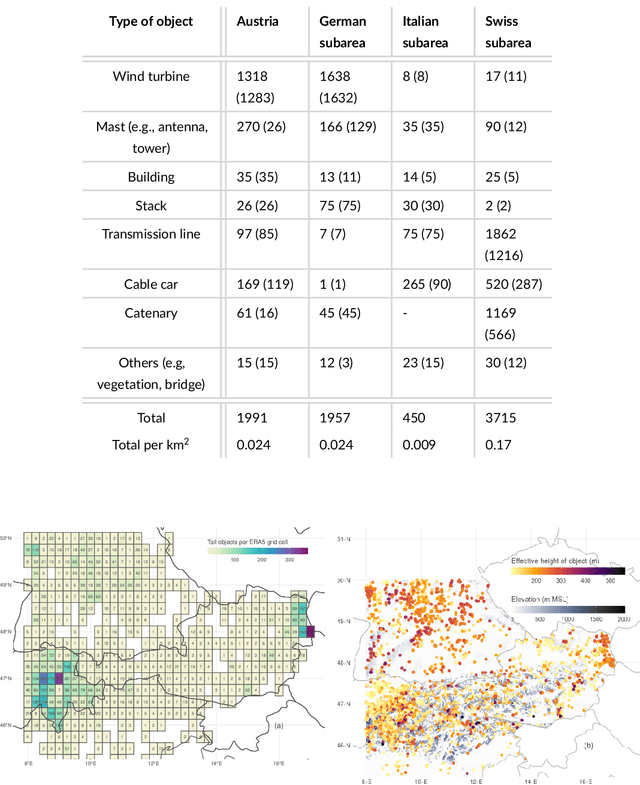
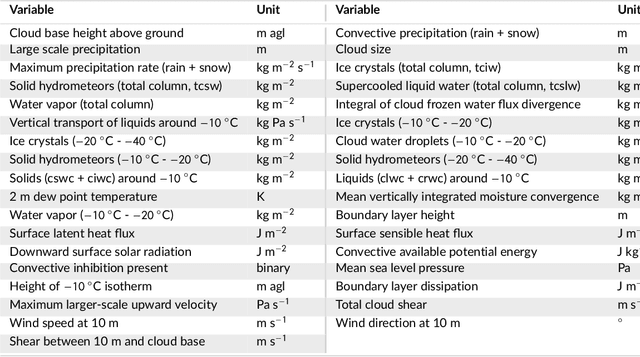
This study investigates lightning at tall objects and evaluates the risk of upward lightning (UL) over the eastern Alps and its surrounding areas. While uncommon, UL poses a threat, especially to wind turbines, as the long-duration current of UL can cause significant damage. Current risk assessment methods overlook the impact of meteorological conditions, potentially underestimating UL risks. Therefore, this study employs random forests, a machine learning technique, to analyze the relationship between UL measured at Gaisberg Tower (Austria) and $35$ larger-scale meteorological variables. Of these, the larger-scale upward velocity, wind speed and direction at 10 meters and cloud physics variables contribute most information. The random forests predict the risk of UL across the study area at a 1 km$^2$ resolution. Strong near-surface winds combined with upward deflection by elevated terrain increase UL risk. The diurnal cycle of the UL risk as well as high-risk areas shift seasonally. They are concentrated north/northeast of the Alps in winter due to prevailing northerly winds, and expanding southward, impacting northern Italy in the transitional and summer months. The model performs best in winter, with the highest predicted UL risk coinciding with observed peaks in measured lightning at tall objects. The highest concentration is north of the Alps, where most wind turbines are located, leading to an increase in overall lightning activity. Comprehensive meteorological information is essential for UL risk assessment, as lightning densities are a poor indicator of lightning at tall objects.

Subgroup detection in linear growth curve models with generalized linear mixed model (GLMM) trees

Growth curve models are popular tools for studying the development of a response variable within subjects over time. Heterogeneity between subjects is common in such models, and researchers are typically interested in explaining or predicting this heterogeneity. We show how generalized linear mixed effects model (GLMM) trees can be used to identify subgroups with differently shaped trajectories in linear growth curve models. Originally developed for clustered cross-sectional data, GLMM trees are extended here to longitudinal data. The resulting extended GLMM trees are directly applicable to growth curve models as an important special case. In simulated and real-world data, we assess the performance of the extensions and compare against other partitioning methods for growth curve models. Extended GLMM trees perform more accurately than the original algorithm and LongCART, and similarly accurate as structural equation model (SEM) trees. In addition, GLMM trees allow for modeling both discrete and continuous time series, are less sensitive to (mis-)specification of the random-effects structure and are much faster to compute.

Upward lightning at wind turbines: Risk assessment from larger-scale meteorology

Upward lightning (UL) has become an increasingly important threat to wind turbines as ever more of them are being installed for renewably producing electricity. The taller the wind turbine the higher the risk that the type of lightning striking the man-made structure is UL. UL can be much more destructive than downward lightning due to its long lasting initial continuous current leading to a large charge transfer within the lightning discharge process. Current standards for the risk assessment of lightning at wind turbines mainly take the summer lightning activity into account, which is inferred from LLS. Ground truth lightning current measurements reveal that less than 50% of UL might be detected by lightning location systems (LLS). This leads to a large underestimation of the proportion of LLS-non-detectable UL at wind turbines, which is the dominant lightning type in the cold season. This study aims to assess the risk of LLS-detectable and LLS-non-detectable UL at wind turbines using direct UL measurements at the Gaisberg Tower (Austria) and S\"antis Tower (Switzerland). Direct UL observations are linked to meteorological reanalysis data and joined by random forests, a powerful machine learning technique. The meteorological drivers for the non-/occurrence of LLS-detectable and LLS-non-detectable UL, respectively, are found from the random forest models trained at the towers and have large predictive skill on independent data. In a second step the results from the tower-trained models are extended to a larger study domain (Central and Northern Germany). The tower-trained models for LLS-detectable lightning is independently verified at wind turbine locations in that domain and found to reliably diagnose that type of UL. Risk maps based on case study events show that high diagnosed probabilities in the study domain coincide with actual UL events.

What Makes Forest-Based Heterogeneous Treatment Effect Estimators Work?

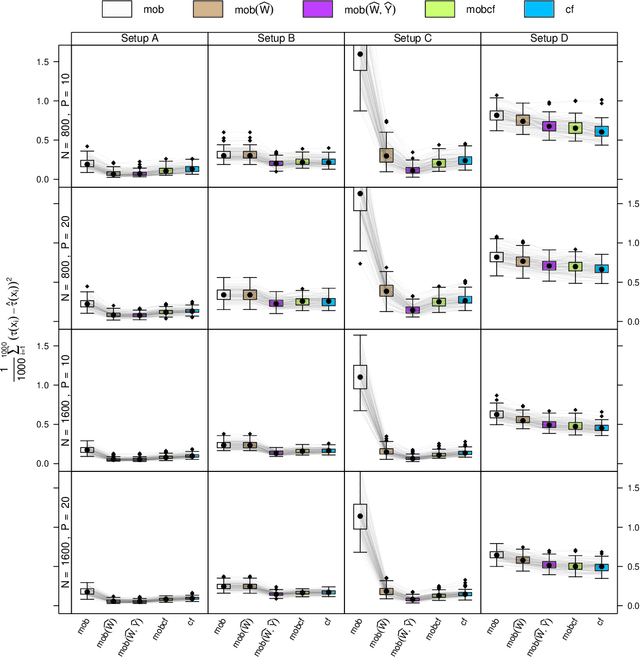
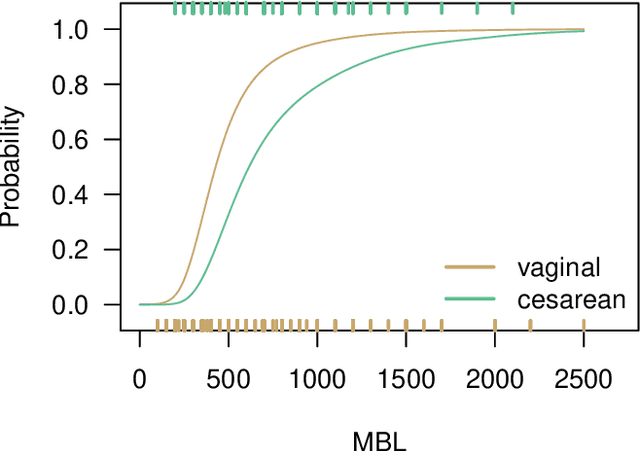
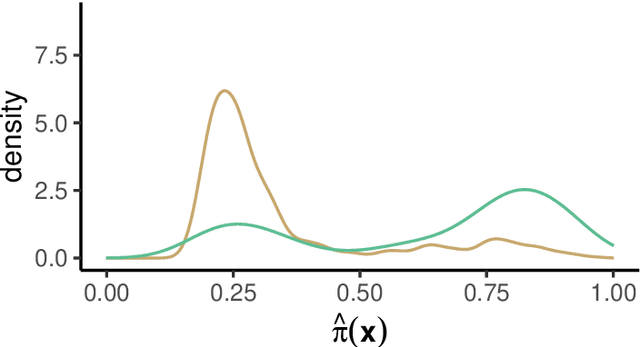
Estimation of heterogeneous treatment effects (HTE) is of prime importance in many disciplines, ranging from personalized medicine to economics among many others. Random forests have been shown to be a flexible and powerful approach to HTE estimation in both randomized trials and observational studies. In particular "causal forests", introduced by Athey, Tibshirani and Wager (2019), along with the R implementation in package grf were rapidly adopted. A related approach, called "model-based forests", that is geared towards randomized trials and simultaneously captures effects of both prognostic and predictive variables, was introduced by Seibold, Zeileis and Hothorn (2018) along with a modular implementation in the R package model4you. Here, we present a unifying view that goes beyond the theoretical motivations and investigates which computational elements make causal forests so successful and how these can be blended with the strengths of model-based forests. To do so, we show that both methods can be understood in terms of the same parameters and model assumptions for an additive model under L2 loss. This theoretical insight allows us to implement several flavors of "model-based causal forests" and dissect their different elements in silico. The original causal forests and model-based forests are compared with the new blended versions in a benchmark study exploring both randomized trials and observational settings. In the randomized setting, both approaches performed akin. If confounding was present in the data generating process, we found local centering of the treatment indicator with the corresponding propensities to be the main driver for good performance. Local centering of the outcome was less important, and might be replaced or enhanced by simultaneous split selection with respect to both prognostic and predictive effects.

Hybrid Machine Learning Forecasts for the UEFA EURO 2020

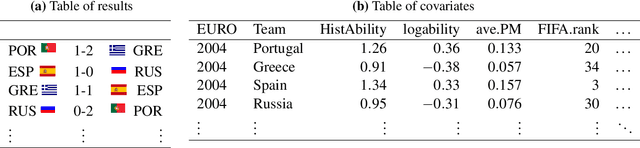
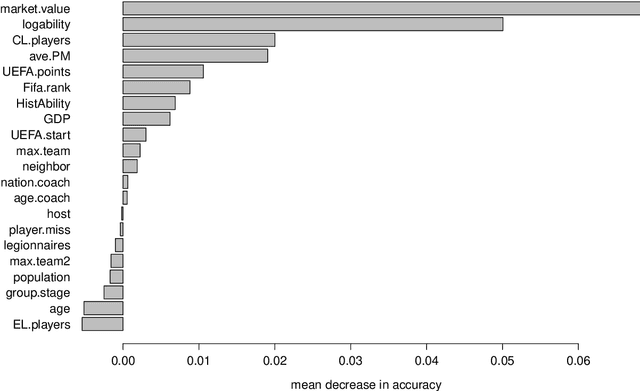
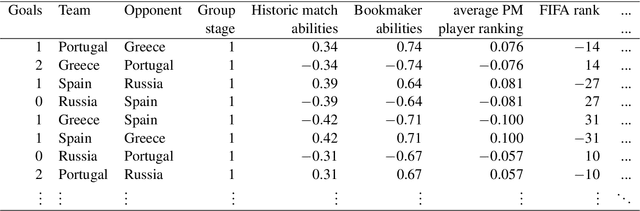
Three state-of-the-art statistical ranking methods for forecasting football matches are combined with several other predictors in a hybrid machine learning model. Namely an ability estimate for every team based on historic matches; an ability estimate for every team based on bookmaker consensus; average plus-minus player ratings based on their individual performances in their home clubs and national teams; and further team covariates (e.g., market value, team structure) and country-specific socio-economic factors (population, GDP). The proposed combined approach is used for learning the number of goals scored in the matches from the four previous UEFA EUROs 2004-2016 and then applied to current information to forecast the upcoming UEFA EURO 2020. Based on the resulting estimates, the tournament is simulated repeatedly and winning probabilities are obtained for all teams. A random forest model favors the current World Champion France with a winning probability of 14.8% before England (13.5%) and Spain (12.3%). Additionally, we provide survival probabilities for all teams and at all tournament stages.

bamlss: A Lego Toolbox for Flexible Bayesian Regression

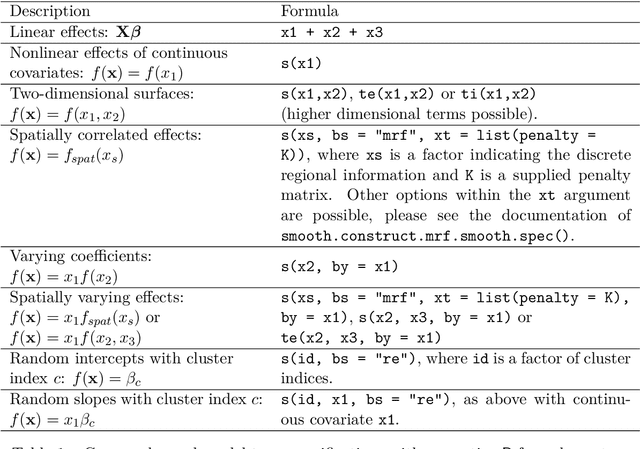
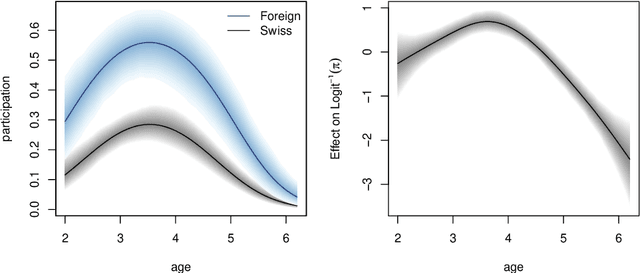
Over the last decades, the challenges in applied regression and in predictive modeling have been changing considerably: (1) More flexible model specifications are needed as big(ger) data become available, facilitated by more powerful computing infrastructure. (2) Full probabilistic modeling rather than predicting just means or expectations is crucial in many applications. (3) Interest in Bayesian inference has been increasing both as an appealing framework for regularizing or penalizing model estimation as well as a natural alternative to classical frequentist inference. However, while there has been a lot of research in all three areas, also leading to associated software packages, a modular software implementation that allows to easily combine all three aspects has not yet been available. For filling this gap, the R package bamlss is introduced for Bayesian additive models for location, scale, and shape (and beyond). At the core of the package are algorithms for highly-efficient Bayesian estimation and inference that can be applied to generalized additive models (GAMs) or generalized additive models for location, scale, and shape (GAMLSS), also known as distributional regression. However, its building blocks are designed as "Lego bricks" encompassing various distributions (exponential family, Cox, joint models, ...), regression terms (linear, splines, random effects, tensor products, spatial fields, ...), and estimators (MCMC, backfitting, gradient boosting, lasso, ...). It is demonstrated how these can be easily recombined to make classical models more flexible or create new custom models for specific modeling challenges.

Hybrid Machine Learning Forecasts for the FIFA Women's World Cup 2019

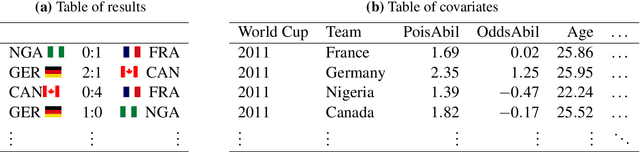
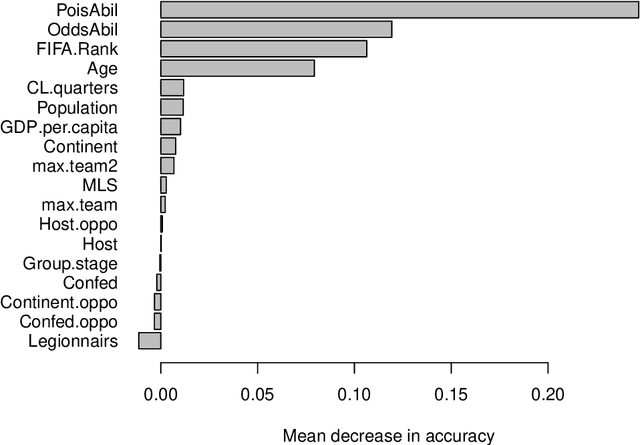
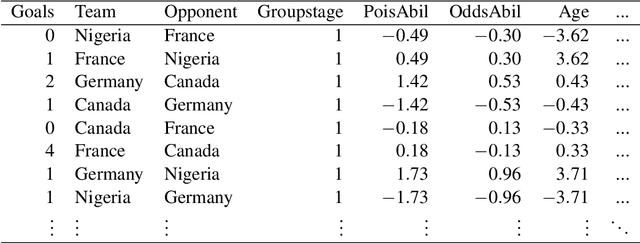
In this work, we combine two different ranking methods together with several other predictors in a joint random forest approach for the scores of soccer matches. The first ranking method is based on the bookmaker consensus, the second ranking method estimates adequate ability parameters that reflect the current strength of the teams best. The proposed combined approach is then applied to the data from the two previous FIFA Women's World Cups 2011 and 2015. Finally, based on the resulting estimates, the FIFA Women's World Cup 2019 is simulated repeatedly and winning probabilities are obtained for all teams. The model clearly favors the defending champion USA before the host France.

Transformation Forests

Regression models for supervised learning problems with a continuous target are commonly understood as models for the conditional mean of the target given predictors. This notion is simple and therefore appealing for interpretation and visualisation. Information about the whole underlying conditional distribution is, however, not available from these models. A more general understanding of regression models as models for conditional distributions allows much broader inference from such models, for example the computation of prediction intervals. Several random forest-type algorithms aim at estimating conditional distributions, most prominently quantile regression forests (Meinshausen, 2006, JMLR). We propose a novel approach based on a parametric family of distributions characterised by their transformation function. A dedicated novel "transformation tree" algorithm able to detect distributional changes is developed. Based on these transformation trees, we introduce "transformation forests" as an adaptive local likelihood estimator of conditional distribution functions. The resulting models are fully parametric yet very general and allow broad inference procedures, such as the model-based bootstrap, to be applied in a straightforward way.