Spatio-seasonal risk assessment of upward lightning at tall objects using meteorological reanalysis data

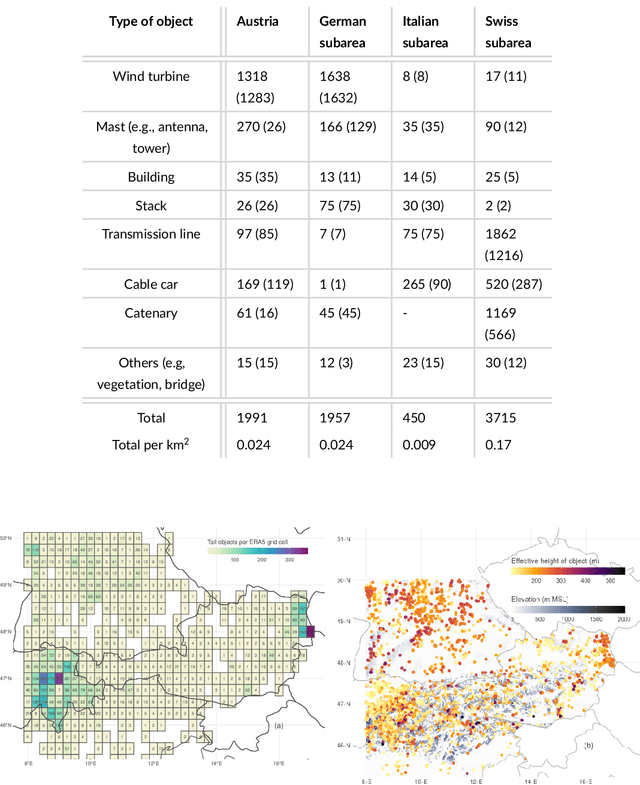
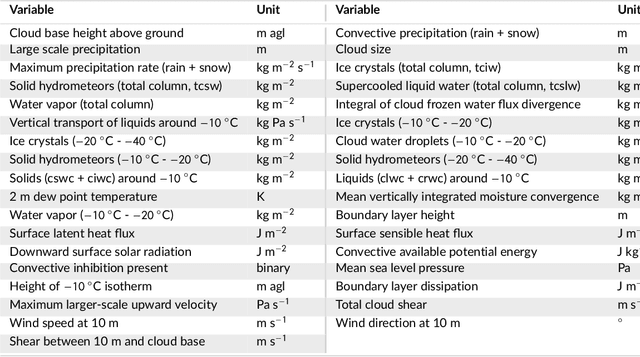
This study investigates lightning at tall objects and evaluates the risk of upward lightning (UL) over the eastern Alps and its surrounding areas. While uncommon, UL poses a threat, especially to wind turbines, as the long-duration current of UL can cause significant damage. Current risk assessment methods overlook the impact of meteorological conditions, potentially underestimating UL risks. Therefore, this study employs random forests, a machine learning technique, to analyze the relationship between UL measured at Gaisberg Tower (Austria) and $35$ larger-scale meteorological variables. Of these, the larger-scale upward velocity, wind speed and direction at 10 meters and cloud physics variables contribute most information. The random forests predict the risk of UL across the study area at a 1 km$^2$ resolution. Strong near-surface winds combined with upward deflection by elevated terrain increase UL risk. The diurnal cycle of the UL risk as well as high-risk areas shift seasonally. They are concentrated north/northeast of the Alps in winter due to prevailing northerly winds, and expanding southward, impacting northern Italy in the transitional and summer months. The model performs best in winter, with the highest predicted UL risk coinciding with observed peaks in measured lightning at tall objects. The highest concentration is north of the Alps, where most wind turbines are located, leading to an increase in overall lightning activity. Comprehensive meteorological information is essential for UL risk assessment, as lightning densities are a poor indicator of lightning at tall objects.

Scalable Estimation for Structured Additive Distributional Regression

Recently, fitting probabilistic models have gained importance in many areas but estimation of such distributional models with very large data sets is a difficult task. In particular, the use of rather complex models can easily lead to memory-related efficiency problems that can make estimation infeasible even on high-performance computers. We therefore propose a novel backfitting algorithm, which is based on the ideas of stochastic gradient descent and can deal virtually with any amount of data on a conventional laptop. The algorithm performs automatic selection of variables and smoothing parameters, and its performance is in most cases superior or at least equivalent to other implementations for structured additive distributional regression, e.g., gradient boosting, while maintaining low computation time. Performance is evaluated using an extensive simulation study and an exceptionally challenging and unique example of lightning count prediction over Austria. A very large dataset with over 9 million observations and 80 covariates is used, so that a prediction model cannot be estimated with standard distributional regression methods but with our new approach.

Upward lightning at wind turbines: Risk assessment from larger-scale meteorology

Upward lightning (UL) has become an increasingly important threat to wind turbines as ever more of them are being installed for renewably producing electricity. The taller the wind turbine the higher the risk that the type of lightning striking the man-made structure is UL. UL can be much more destructive than downward lightning due to its long lasting initial continuous current leading to a large charge transfer within the lightning discharge process. Current standards for the risk assessment of lightning at wind turbines mainly take the summer lightning activity into account, which is inferred from LLS. Ground truth lightning current measurements reveal that less than 50% of UL might be detected by lightning location systems (LLS). This leads to a large underestimation of the proportion of LLS-non-detectable UL at wind turbines, which is the dominant lightning type in the cold season. This study aims to assess the risk of LLS-detectable and LLS-non-detectable UL at wind turbines using direct UL measurements at the Gaisberg Tower (Austria) and S\"antis Tower (Switzerland). Direct UL observations are linked to meteorological reanalysis data and joined by random forests, a powerful machine learning technique. The meteorological drivers for the non-/occurrence of LLS-detectable and LLS-non-detectable UL, respectively, are found from the random forest models trained at the towers and have large predictive skill on independent data. In a second step the results from the tower-trained models are extended to a larger study domain (Central and Northern Germany). The tower-trained models for LLS-detectable lightning is independently verified at wind turbine locations in that domain and found to reliably diagnose that type of UL. Risk maps based on case study events show that high diagnosed probabilities in the study domain coincide with actual UL events.

bamlss: A Lego Toolbox for Flexible Bayesian Regression

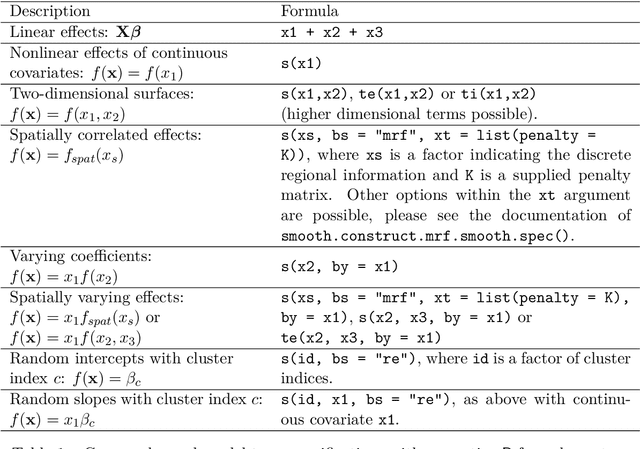
Over the last decades, the challenges in applied regression and in predictive modeling have been changing considerably: (1) More flexible model specifications are needed as big(ger) data become available, facilitated by more powerful computing infrastructure. (2) Full probabilistic modeling rather than predicting just means or expectations is crucial in many applications. (3) Interest in Bayesian inference has been increasing both as an appealing framework for regularizing or penalizing model estimation as well as a natural alternative to classical frequentist inference. However, while there has been a lot of research in all three areas, also leading to associated software packages, a modular software implementation that allows to easily combine all three aspects has not yet been available. For filling this gap, the R package bamlss is introduced for Bayesian additive models for location, scale, and shape (and beyond). At the core of the package are algorithms for highly-efficient Bayesian estimation and inference that can be applied to generalized additive models (GAMs) or generalized additive models for location, scale, and shape (GAMLSS), also known as distributional regression. However, its building blocks are designed as "Lego bricks" encompassing various distributions (exponential family, Cox, joint models, ...), regression terms (linear, splines, random effects, tensor products, spatial fields, ...), and estimators (MCMC, backfitting, gradient boosting, lasso, ...). It is demonstrated how these can be easily recombined to make classical models more flexible or create new custom models for specific modeling challenges.