Stagewise Boosting Distributional Regression

Forward stagewise regression is a simple algorithm that can be used to estimate regularized models. The updating rule adds a small constant to a regression coefficient in each iteration, such that the underlying optimization problem is solved slowly with small improvements. This is similar to gradient boosting, with the essential difference that the step size is determined by the product of the gradient and a step length parameter in the latter algorithm. One often overlooked challenge in gradient boosting for distributional regression is the issue of a vanishing small gradient, which practically halts the algorithm's progress. We show that gradient boosting in this case oftentimes results in suboptimal models, especially for complex problems certain distributional parameters are never updated due to the vanishing gradient. Therefore, we propose a stagewise boosting-type algorithm for distributional regression, combining stagewise regression ideas with gradient boosting. Additionally, we extend it with a novel regularization method, correlation filtering, to provide additional stability when the problem involves a large number of covariates. Furthermore, the algorithm includes best-subset selection for parameters and can be applied to big data problems by leveraging stochastic approximations of the updating steps. Besides the advantage of processing large datasets, the stochastic nature of the approximations can lead to better results, especially for complex distributions, by reducing the risk of being trapped in a local optimum. The performance of our proposed stagewise boosting distributional regression approach is investigated in an extensive simulation study and by estimating a full probabilistic model for lightning counts with data of more than 9.1 million observations and 672 covariates.

Scalable Estimation for Structured Additive Distributional Regression

Recently, fitting probabilistic models have gained importance in many areas but estimation of such distributional models with very large data sets is a difficult task. In particular, the use of rather complex models can easily lead to memory-related efficiency problems that can make estimation infeasible even on high-performance computers. We therefore propose a novel backfitting algorithm, which is based on the ideas of stochastic gradient descent and can deal virtually with any amount of data on a conventional laptop. The algorithm performs automatic selection of variables and smoothing parameters, and its performance is in most cases superior or at least equivalent to other implementations for structured additive distributional regression, e.g., gradient boosting, while maintaining low computation time. Performance is evaluated using an extensive simulation study and an exceptionally challenging and unique example of lightning count prediction over Austria. A very large dataset with over 9 million observations and 80 covariates is used, so that a prediction model cannot be estimated with standard distributional regression methods but with our new approach.

Distributional Adaptive Soft Regression Trees

Random forests are an ensemble method relevant for many problems, such as regression or classification. They are popular due to their good predictive performance (compared to, e.g., decision trees) requiring only minimal tuning of hyperparameters. They are built via aggregation of multiple regression trees during training and are usually calculated recursively using hard splitting rules. Recently regression forests have been incorporated into the framework of distributional regression, a nowadays popular regression approach aiming at estimating complete conditional distributions rather than relating the mean of an output variable to input features only - as done classically. This article proposes a new type of a distributional regression tree using a multivariate soft split rule. One great advantage of the soft split is that smooth high-dimensional functions can be estimated with only one tree while the complexity of the function is controlled adaptive by information criteria. Moreover, the search for the optimal split variable is obsolete. We show by means of extensive simulation studies that the algorithm has excellent properties and outperforms various benchmark methods, especially in the presence of complex non-linear feature interactions. Finally, we illustrate the usefulness of our approach with an example on probabilistic forecasts for the Sun's activity.

bamlss: A Lego Toolbox for Flexible Bayesian Regression

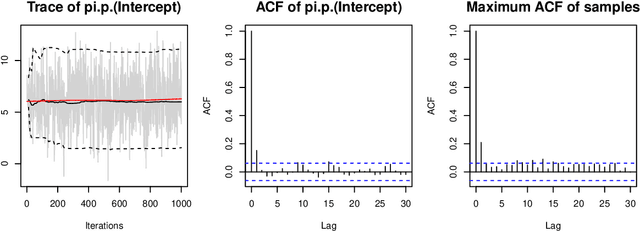
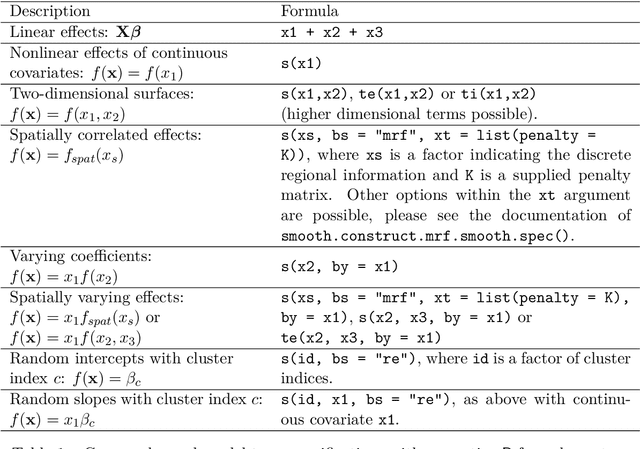
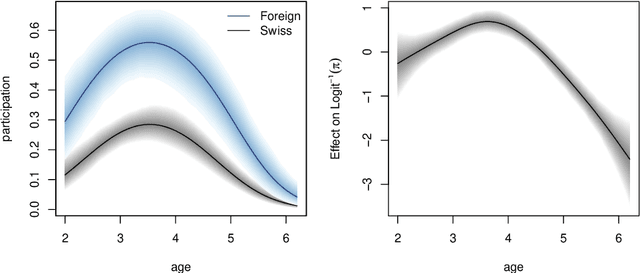
Over the last decades, the challenges in applied regression and in predictive modeling have been changing considerably: (1) More flexible model specifications are needed as big(ger) data become available, facilitated by more powerful computing infrastructure. (2) Full probabilistic modeling rather than predicting just means or expectations is crucial in many applications. (3) Interest in Bayesian inference has been increasing both as an appealing framework for regularizing or penalizing model estimation as well as a natural alternative to classical frequentist inference. However, while there has been a lot of research in all three areas, also leading to associated software packages, a modular software implementation that allows to easily combine all three aspects has not yet been available. For filling this gap, the R package bamlss is introduced for Bayesian additive models for location, scale, and shape (and beyond). At the core of the package are algorithms for highly-efficient Bayesian estimation and inference that can be applied to generalized additive models (GAMs) or generalized additive models for location, scale, and shape (GAMLSS), also known as distributional regression. However, its building blocks are designed as "Lego bricks" encompassing various distributions (exponential family, Cox, joint models, ...), regression terms (linear, splines, random effects, tensor products, spatial fields, ...), and estimators (MCMC, backfitting, gradient boosting, lasso, ...). It is demonstrated how these can be easily recombined to make classical models more flexible or create new custom models for specific modeling challenges.