On the rate of convergence of fully connected very deep neural network regression estimates

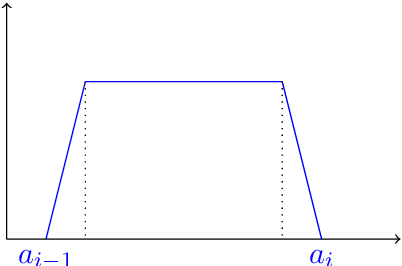
Recent results in nonparametric regression show that deep learning, i.e., neural networks estimates with many hidden layers, are able to circumvent the so-called curse of dimensionality in case that suitable restrictions on the structure of the regression function hold. One key feature of the neural networks used in these results is that they are not fully connected. In this paper we show that we can get similar results also for fully connected multilayer feedforward neural networks with ReLU activation functions, provided the number of neurons per hidden layer is fixed and the number of hidden layers tends to infinity for sample size tending to infinity. The proof is based on new approximation results concerning fully connected deep neural networks.