Understanding the Effect of GCN Convolutions in Regression Tasks

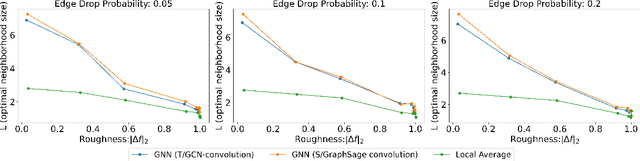
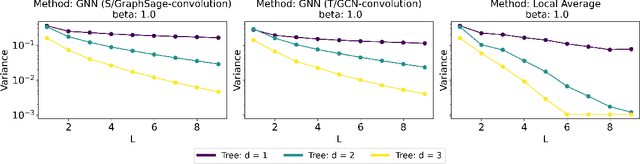
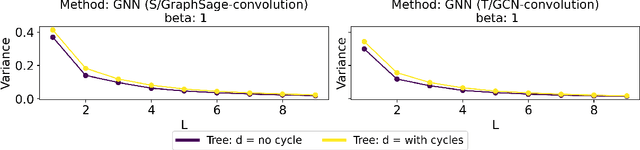
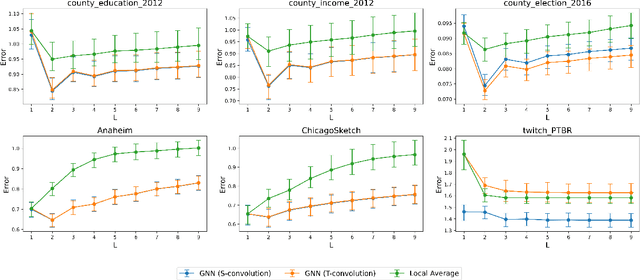
Graph Convolutional Networks (GCNs) have become a pivotal method in machine learning for modeling functions over graphs. Despite their widespread success across various applications, their statistical properties (e.g. consistency, convergence rates) remain ill-characterized. To begin addressing this knowledge gap, in this paper, we provide a formal analysis of the impact of convolution operators on regression tasks over homophilic networks. Focusing on estimators based solely on neighborhood aggregation, we examine how two common convolutions - the original GCN and GraphSage convolutions - affect the learning error as a function of the neighborhood topology and the number of convolutional layers. We explicitly characterize the bias-variance trade-off incurred by GCNs as a function of the neighborhood size and identify specific graph topologies where convolution operators are less effective. Our theoretical findings are corroborated by synthetic experiments, and provide a start to a deeper quantitative understanding of convolutional effects in GCNs for offering rigorous guidelines for practitioners.

Link Prediction in the Stochastic Block Model with Outliers

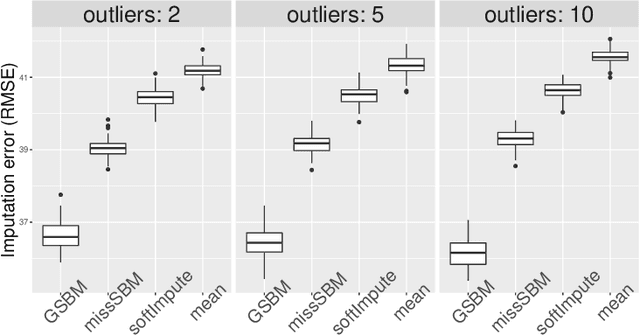
The Stochastic Block Model is a popular model for network analysis in the presence of community structure. However, in numerous examples, the assumptions underlying this classical model are put in default by the behaviour of a small number of outlier nodes such as hubs, nodes with mixed membership profiles, or corrupted nodes. In addition, real-life networks are likely to be incomplete, due to non-response or machine failures. We introduce a new algorithm to estimate the connection probabilities in a network, which is robust to both outlier nodes and missing observations. Under fairly general assumptions, this method detects the outliers, and achieves the best known error for the estimation of connection probabilities with polynomial computation cost. In addition, we prove sub-linear convergence of our algorithm. We provide a simulation study which demonstrates the good behaviour of the method in terms of outliers selection and prediction of the missing links.

Low-rank Interaction with Sparse Additive Effects Model for Large Data Frames

Many applications of machine learning involve the analysis of large data frames-matrices collecting heterogeneous measurements (binary, numerical, counts, etc.) across samples-with missing values. Low-rank models, as studied by Udell et al. [30], are popular in this framework for tasks such as visualization, clustering and missing value imputation. Yet, available methods with statistical guarantees and efficient optimization do not allow explicit modeling of main additive effects such as row and column, or covariate effects. In this paper, we introduce a low-rank interaction and sparse additive effects (LORIS) model which combines matrix regression on a dictionary and low-rank design, to estimate main effects and interactions simultaneously. We provide statistical guarantees in the form of upper bounds on the estimation error of both components. Then, we introduce a mixed coordinate gradient descent (MCGD) method which provably converges sub-linearly to an optimal solution and is computationally efficient for large scale data sets. We show on simulated and survey data that the method has a clear advantage over current practices, which consist in dealing separately with additive effects in a preprocessing step.

Collective Matrix Completion

Matrix completion aims to reconstruct a data matrix based on observations of a small number of its entries. Usually in matrix completion a single matrix is considered, which can be, for example, a rating matrix in recommendation system. However, in practical situations, data is often obtained from multiple sources which results in a collection of matrices rather than a single one. In this work, we consider the problem of collective matrix completion with multiple and heterogeneous matrices, which can be count, binary, continuous, etc. We first investigate the setting where, for each source, the matrix entries are sampled from an exponential family distribution. Then, we relax the assumption of exponential family distribution for the noise and we investigate the distribution-free case. In this setting, we do not assume any specific model for the observations. The estimation procedures are based on minimizing the sum of a goodness-of-fit term and the nuclear norm penalization of the whole collective matrix. We prove that the proposed estimators achieve fast rates of convergence under the two considered settings and we corroborate our results with numerical experiments.

Probabilistic low-rank matrix completion on finite alphabets

The task of reconstructing a matrix given a sample of observedentries is known as the matrix completion problem. It arises ina wide range of problems, including recommender systems, collaborativefiltering, dimensionality reduction, image processing, quantum physics or multi-class classificationto name a few. Most works have focused on recovering an unknown real-valued low-rankmatrix from randomly sub-sampling its entries.Here, we investigate the case where the observations take a finite number of values, corresponding for examples to ratings in recommender systems or labels in multi-class classification.We also consider a general sampling scheme (not necessarily uniform) over the matrix entries.The performance of a nuclear-norm penalized estimator is analyzed theoretically.More precisely, we derive bounds for the Kullback-Leibler divergence between the true and estimated distributions.In practice, we have also proposed an efficient algorithm based on lifted coordinate gradient descent in order to tacklepotentially high dimensional settings.

Adaptive Multinomial Matrix Completion

The task of estimating a matrix given a sample of observed entries is known as the \emph{matrix completion problem}. Most works on matrix completion have focused on recovering an unknown real-valued low-rank matrix from a random sample of its entries. Here, we investigate the case of highly quantized observations when the measurements can take only a small number of values. These quantized outputs are generated according to a probability distribution parametrized by the unknown matrix of interest. This model corresponds, for example, to ratings in recommender systems or labels in multi-class classification. We consider a general, non-uniform, sampling scheme and give theoretical guarantees on the performance of a constrained, nuclear norm penalized maximum likelihood estimator. One important advantage of this estimator is that it does not require knowledge of the rank or an upper bound on the nuclear norm of the unknown matrix and, thus, it is adaptive. We provide lower bounds showing that our estimator is minimax optimal. An efficient algorithm based on lifted coordinate gradient descent is proposed to compute the estimator. A limited Monte-Carlo experiment, using both simulated and real data is provided to support our claims.