Tuning the Geometry of Graph Neural Networks
Paper and Code
Jul 12, 2022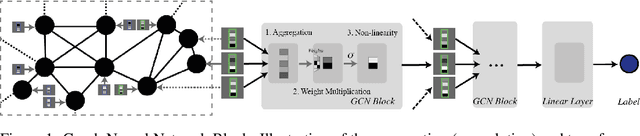
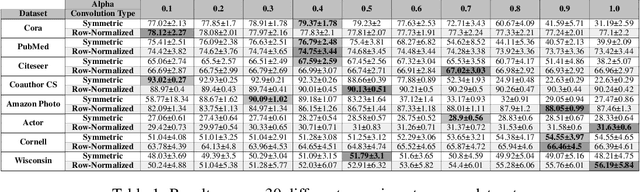
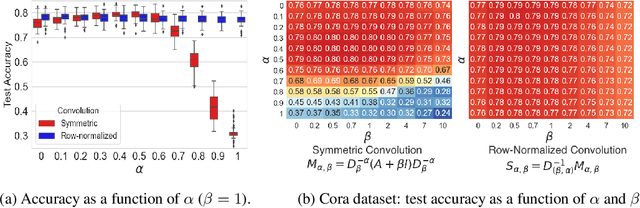

By recursively summing node features over entire neighborhoods, spatial graph convolution operators have been heralded as key to the success of Graph Neural Networks (GNNs). Yet, despite the multiplication of GNN methods across tasks and applications, the impact of this aggregation operation on their performance still has yet to be extensively analysed. In fact, while efforts have mostly focused on optimizing the architecture of the neural network, fewer works have attempted to characterize (a) the different classes of spatial convolution operators, (b) how the choice of a particular class relates to properties of the data , and (c) its impact on the geometry of the embedding space. In this paper, we propose to answer all three questions by dividing existing operators into two main classes ( symmetrized vs. row-normalized spatial convolutions), and show how these translate into different implicit biases on the nature of the data. Finally, we show that this aggregation operator is in fact tunable, and explicit regimes in which certain choices of operators -- and therefore, embedding geometries -- might be more appropriate.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge