UniGrasp: Learning a Unified Model to Grasp with N-Fingered Robotic Hands

To achieve a successful grasp, gripper attributes including geometry and kinematics play a role equally important to the target object geometry. The majority of previous work has focused on developing grasp methods that generalize over novel object geometry but are specific to a certain robot hand. We propose UniGrasp, an efficient data-driven grasp synthesis method that considers both the object geometry and gripper attributes as inputs. UniGrasp is based on a novel deep neural network architecture that selects sets of contact points from the input point cloud of the object. The proposed model is trained on a large dataset to produce contact points that are in force closure and reachable by the robot hand. By using contact points as output, we can transfer between a diverse set of N-fingered robotic hands. Our model produces over 90 percent valid contact points in Top10 predictions in simulation and more than 90 percent successful grasps in the real world experiments for various known two-fingered and three-fingered grippers. Our model also achieves 93 percent and 83 percent successful grasps in the real world experiments for a novel two-fingered and five-fingered anthropomorphic robotic hand, respectively.

geomstats: a Python Package for Riemannian Geometry in Machine Learning

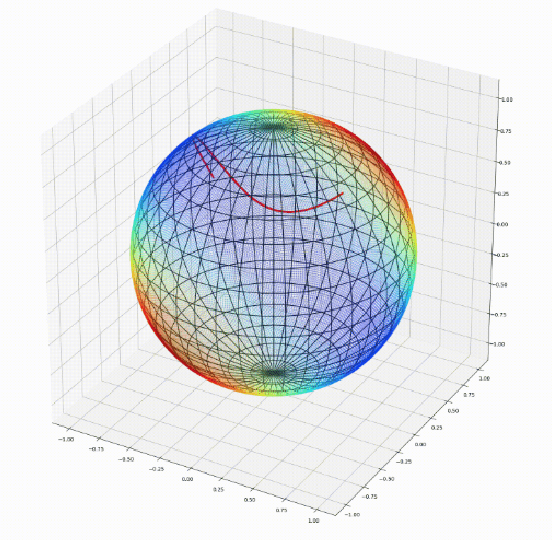
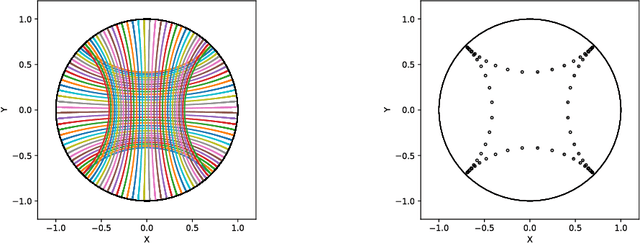
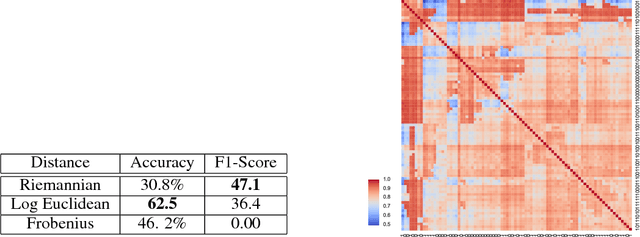
We introduce geomstats, a python package that performs computations on manifolds such as hyperspheres, hyperbolic spaces, spaces of symmetric positive definite matrices and Lie groups of transformations. We provide efficient and extensively unit-tested implementations of these manifolds, together with useful Riemannian metrics and associated Exponential and Logarithm maps. The corresponding geodesic distances provide a range of intuitive choices of Machine Learning loss functions. We also give the corresponding Riemannian gradients. The operations implemented in geomstats are available with different computing backends such as numpy, tensorflow and keras. We have enabled GPU implementation and integrated geomstats manifold computations into keras deep learning framework. This paper also presents a review of manifolds in machine learning and an overview of the geomstats package with examples demonstrating its use for efficient and user-friendly Riemannian geometry.

Real Time Collision Detection and Identification for Robotic Manipulators

The majority of everyday tasks involve interacting with unstructured environments. This implies that, in order for robots to be truly useful they must be able to handle contacts. This paper explores how a particle filter can be used to localize a contact point and estimate the external force. We demonstrate the capability of the particle filter on a simulated 4DoF planar robotic arm, and compare it to a well-established analytical approach.