Neural Backward Filtering Forward Guiding

Inference in non-linear continuous stochastic processes on trees is challenging, particularly when observations are sparse (leaf-only) and the topology is complex. Exact smoothing via Doob's $h$-transform is intractable for general non-linear dynamics, while particle-based methods degrade in high dimensions. We propose Neural Backward Filtering Forward Guiding (NBFFG), a unified framework for both discrete transitions and continuous diffusions. Our method constructs a variational posterior by leveraging an auxiliary linear-Gaussian process. This auxiliary process yields a closed-form backward filter that serves as a ``guide'', steering the generative path toward high-likelihood regions. We then learn a neural residual--parameterized as a normalizing flow or a controlled SDE--to capture the non-linear discrepancies. This formulation allows for an unbiased path-wise subsampling scheme, reducing the training complexity from tree-size dependent to path-length dependent. Empirical results show that NBFFG outperforms baselines on synthetic benchmarks, and we demonstrate the method on a high-dimensional inference task in phylogenetic analysis with reconstruction of ancestral butterfly wing shapes.

Neural Guided Diffusion Bridges

We propose a novel method for simulating conditioned diffusion processes (diffusion bridges) in Euclidean spaces. By training a neural network to approximate bridge dynamics, our approach eliminates the need for computationally intensive Markov Chain Monte Carlo (MCMC) methods or reverse-process modeling. Compared to existing methods, it offers greater robustness across various diffusion specifications and conditioning scenarios. This applies in particular to rare events and multimodal distributions, which pose challenges for score-learning- and MCMC-based approaches. We propose a flexible variational family for approximating the diffusion bridge path measure which is partially specified by a neural network. Once trained, it enables efficient independent sampling at a cost comparable to sampling the unconditioned (forward) process.

Diffusion bridges for stochastic Hamiltonian systems with applications to shape analysis

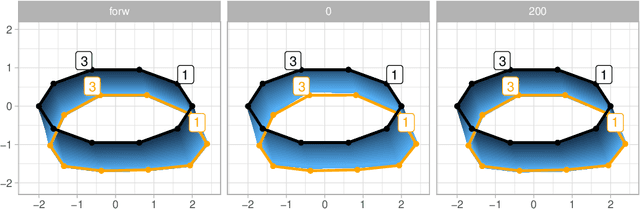
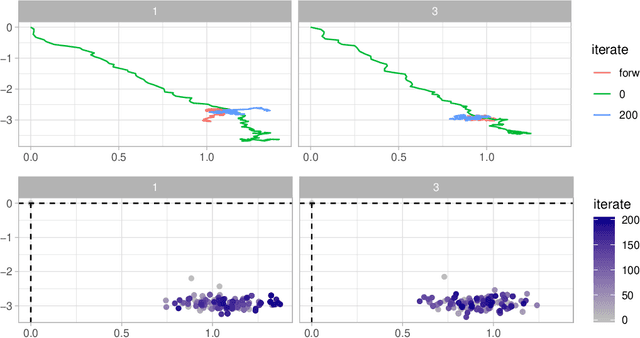
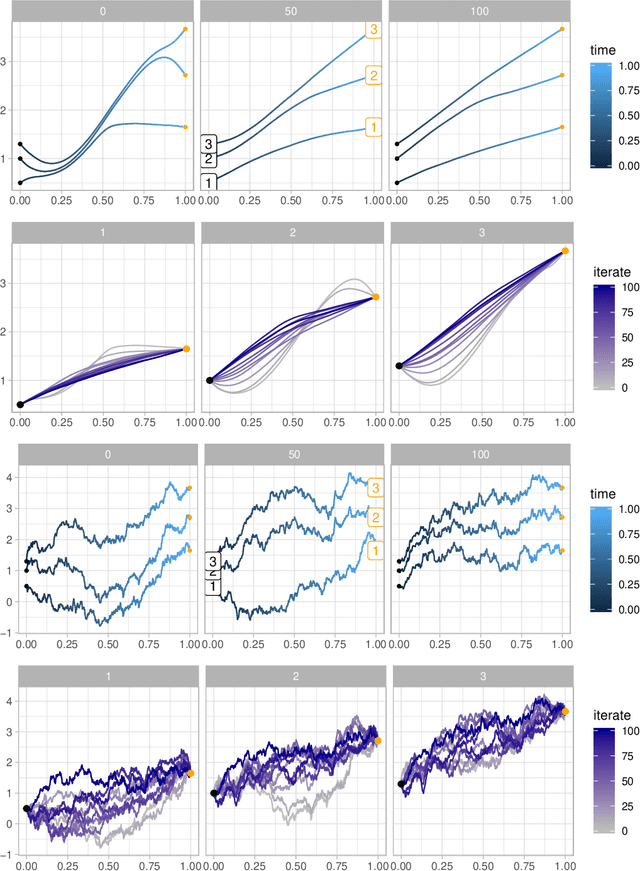
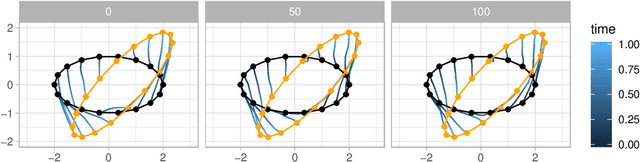
Stochastically evolving geometric systems are studied in geometric mechanics for modelling turbulence parts of multi-scale fluid flows and in shape analysis for stochastic evolutions of shapes of e.g. human organs. Recently introduced models involve stochastic differential equations that govern the dynamics of a diffusion process $X$. In applications $X$ is only partially observed at times $0$ and $T>0$. Conditional on these observations, interest lies in inferring parameters in the dynamics of the diffusion and reconstructing the path $(X_t,\, t\in [0,T])$. The latter problem is known as bridge simulation. We develop a general scheme for bridge sampling in the case of finite dimensional systems of shape landmarks and singular solutions in fluid dynamics. This scheme allows for subsequent statistical inference of properties of the fluid flow or the evolution of observed shapes. It covers stochastic landmark models for which no suitable simulation method has been proposed in the literature, that removes restrictions of earlier approaches, improves the handling of the nonlinearity of the configuration space leading to more effective sampling schemes and allows to generalise the common inexact matching scheme to the stochastic setting.

Nonparametric Bayesian volatility learning under microstructure noise

Aiming at financial applications, we study the problem of learning the volatility under market microstructure noise. Specifically, we consider noisy discrete time observations from a stochastic differential equation and develop a novel computational method to learn the diffusion coefficient of the equation. We take a nonparametric Bayesian approach, where we model the volatility function a priori as piecewise constant. Its prior is specified via the inverse Gamma Markov chain. Sampling from the posterior is accomplished by incorporating the Forward Filtering Backward Simulation algorithm in the Gibbs sampler. Good performance of the method is demonstrated on two representative synthetic data examples. Finally, we apply the method on the EUR/USD exchange rate dataset.