Score matching for bridges without time-reversals

We propose a new algorithm for learning a bridged diffusion process using score-matching methods. Our method relies on reversing the dynamics of the forward process and using this to learn a score function, which, via Doob's $h$-transform, gives us a bridged diffusion process; that is, a process conditioned on an endpoint. In contrast to prior methods, ours learns the score term $\nabla_x \log p(t, x; T, y)$, for given $t, Y$ directly, completely avoiding the need for first learning a time reversal. We compare the performance of our algorithm with existing methods and see that it outperforms using the (learned) time-reversals to learn the score term. The code can be found at https://github.com/libbylbaker/forward_bridge.

Causal structure learning with momentum: Sampling distributions over Markov Equivalence Classes of DAGs

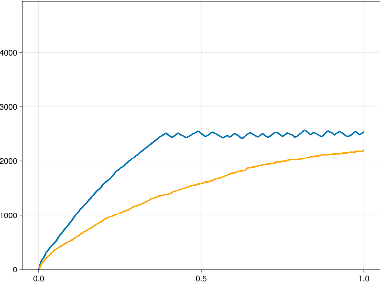
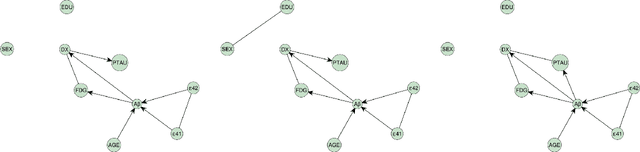
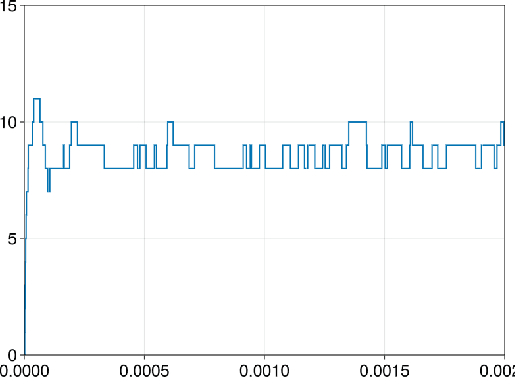
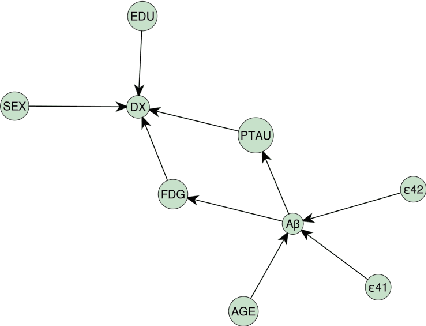
In the context of inferring a Bayesian network structure (directed acyclic graph, DAG for short), we devise a non-reversible continuous time Markov chain, the "Causal Zig-Zag sampler", that targets a probability distribution over classes of observationally equivalent (Markov equivalent) DAGs. The classes are represented as completed partially directed acyclic graphs (CPDAGs). The non-reversible Markov chain relies on the operators used in Chickering's Greedy Equivalence Search (GES) and is endowed with a momentum variable, which improves mixing significantly as we show empirically. The possible target distributions include posterior distributions based on a prior over DAGs and a Markov equivalent likelihood. We offer an efficient implementation wherein we develop new algorithms for listing, counting, uniformly sampling, and applying possible moves of the GES operators, all of which significantly improve upon the state-of-the-art.

Differentiating Metropolis-Hastings to Optimize Intractable Densities

We develop an algorithm for automatic differentiation of Metropolis-Hastings samplers, allowing us to differentiate through probabilistic inference, even if the model has discrete components within it. Our approach fuses recent advances in stochastic automatic differentiation with traditional Markov chain coupling schemes, providing an unbiased and low-variance gradient estimator. This allows us to apply gradient-based optimization to objectives expressed as expectations over intractable target densities. We demonstrate our approach by finding an ambiguous observation in a Gaussian mixture model and by maximizing the specific heat in an Ising model.

Automatic Differentiation of Programs with Discrete Randomness

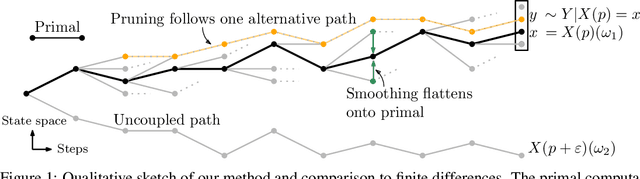
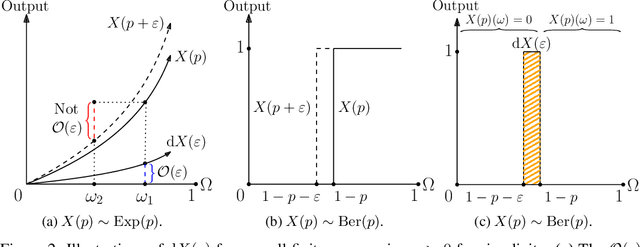
Automatic differentiation (AD), a technique for constructing new programs which compute the derivative of an original program, has become ubiquitous throughout scientific computing and deep learning due to the improved performance afforded by gradient-based optimization. However, AD systems have been restricted to the subset of programs that have a continuous dependence on parameters. Programs that have discrete stochastic behaviors governed by distribution parameters, such as flipping a coin with probability $p$ of being heads, pose a challenge to these systems because the connection between the result (heads vs tails) and the parameters ($p$) is fundamentally discrete. In this paper we develop a new reparameterization-based methodology that allows for generating programs whose expectation is the derivative of the expectation of the original program. We showcase how this method gives an unbiased and low-variance estimator which is as automated as traditional AD mechanisms. We demonstrate unbiased forward-mode AD of discrete-time Markov chains, agent-based models such as Conway's Game of Life, and unbiased reverse-mode AD of a particle filter. Our code is available at https://github.com/gaurav-arya/StochasticAD.jl.

Flexible Group Fairness Metrics for Survival Analysis

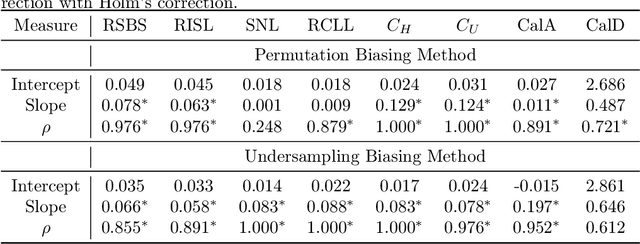
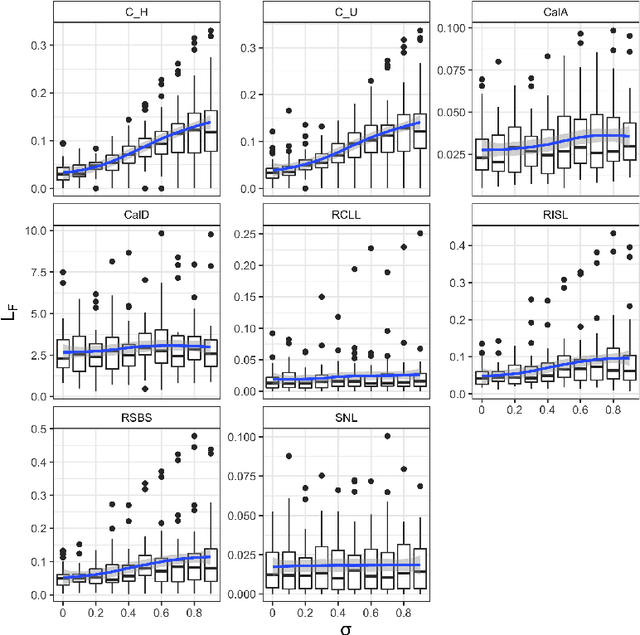
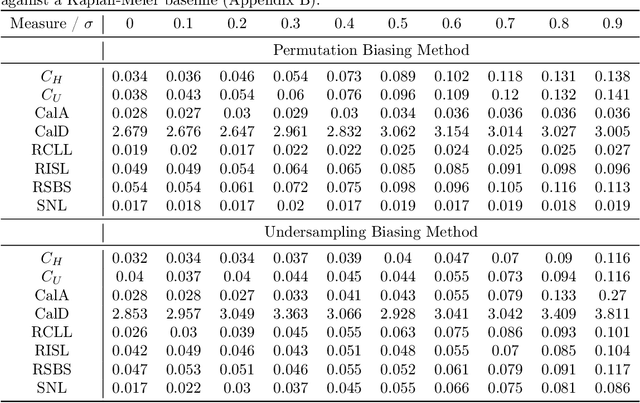
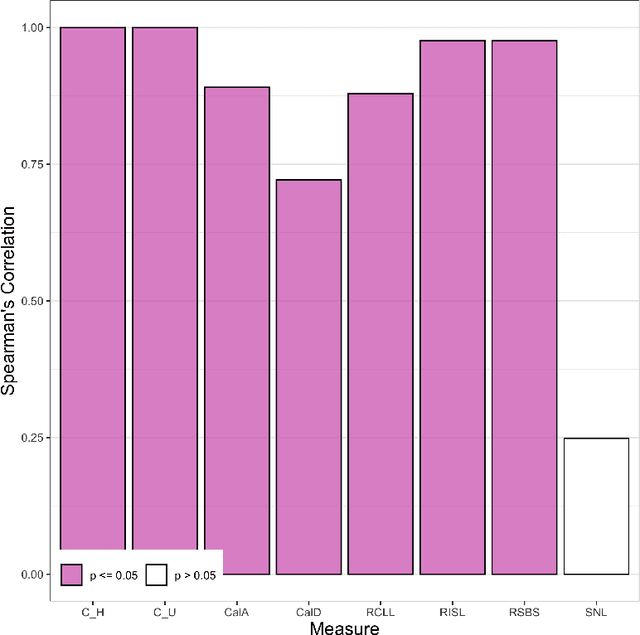
Algorithmic fairness is an increasingly important field concerned with detecting and mitigating biases in machine learning models. There has been a wealth of literature for algorithmic fairness in regression and classification however there has been little exploration of the field for survival analysis. Survival analysis is the prediction task in which one attempts to predict the probability of an event occurring over time. Survival predictions are particularly important in sensitive settings such as when utilising machine learning for diagnosis and prognosis of patients. In this paper we explore how to utilise existing survival metrics to measure bias with group fairness metrics. We explore this in an empirical experiment with 29 survival datasets and 8 measures. We find that measures of discrimination are able to capture bias well whereas there is less clarity with measures of calibration and scoring rules. We suggest further areas for research including prediction-based fairness metrics for distribution predictions.

Diffusion bridges for stochastic Hamiltonian systems with applications to shape analysis

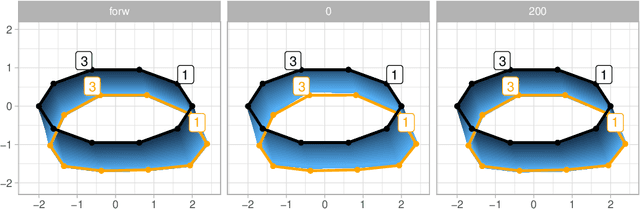
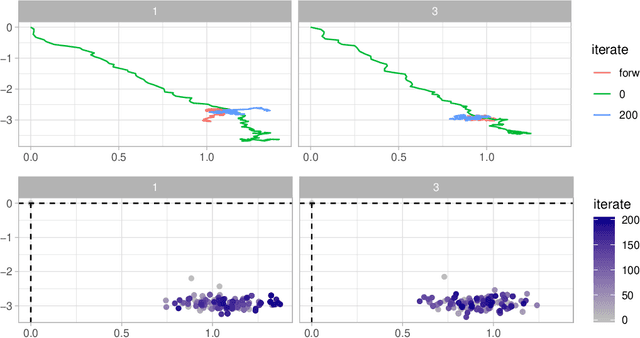
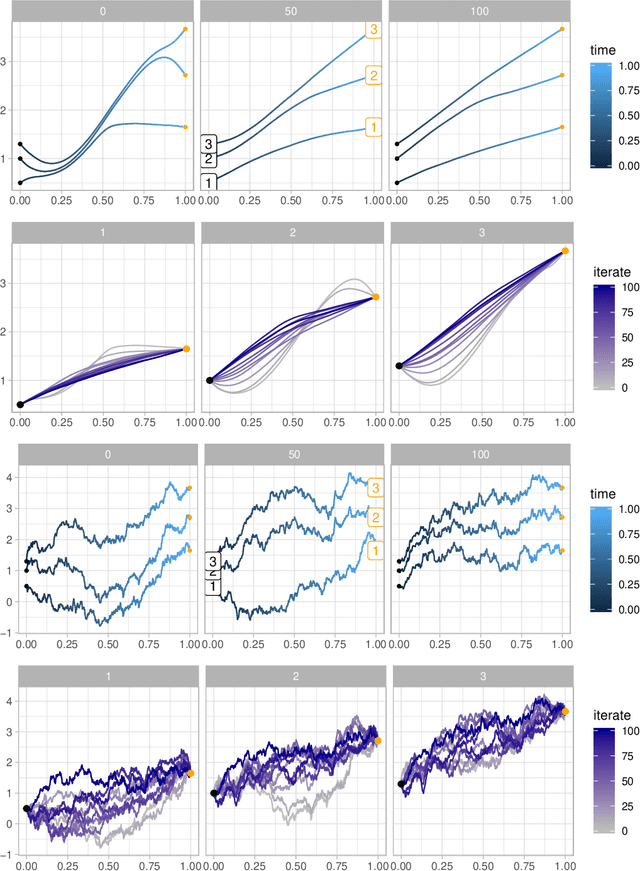
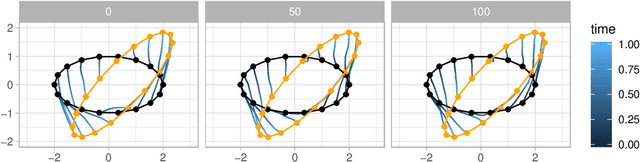
Stochastically evolving geometric systems are studied in geometric mechanics for modelling turbulence parts of multi-scale fluid flows and in shape analysis for stochastic evolutions of shapes of e.g. human organs. Recently introduced models involve stochastic differential equations that govern the dynamics of a diffusion process $X$. In applications $X$ is only partially observed at times $0$ and $T>0$. Conditional on these observations, interest lies in inferring parameters in the dynamics of the diffusion and reconstructing the path $(X_t,\, t\in [0,T])$. The latter problem is known as bridge simulation. We develop a general scheme for bridge sampling in the case of finite dimensional systems of shape landmarks and singular solutions in fluid dynamics. This scheme allows for subsequent statistical inference of properties of the fluid flow or the evolution of observed shapes. It covers stochastic landmark models for which no suitable simulation method has been proposed in the literature, that removes restrictions of earlier approaches, improves the handling of the nonlinearity of the configuration space leading to more effective sampling schemes and allows to generalise the common inexact matching scheme to the stochastic setting.

Nonparametric Bayesian volatility learning under microstructure noise

Aiming at financial applications, we study the problem of learning the volatility under market microstructure noise. Specifically, we consider noisy discrete time observations from a stochastic differential equation and develop a novel computational method to learn the diffusion coefficient of the equation. We take a nonparametric Bayesian approach, where we model the volatility function a priori as piecewise constant. Its prior is specified via the inverse Gamma Markov chain. Sampling from the posterior is accomplished by incorporating the Forward Filtering Backward Simulation algorithm in the Gibbs sampler. Good performance of the method is demonstrated on two representative synthetic data examples. Finally, we apply the method on the EUR/USD exchange rate dataset.