Causal structure learning with momentum: Sampling distributions over Markov Equivalence Classes of DAGs

In the context of inferring a Bayesian network structure (directed acyclic graph, DAG for short), we devise a non-reversible continuous time Markov chain, the "Causal Zig-Zag sampler", that targets a probability distribution over classes of observationally equivalent (Markov equivalent) DAGs. The classes are represented as completed partially directed acyclic graphs (CPDAGs). The non-reversible Markov chain relies on the operators used in Chickering's Greedy Equivalence Search (GES) and is endowed with a momentum variable, which improves mixing significantly as we show empirically. The possible target distributions include posterior distributions based on a prior over DAGs and a Markov equivalent likelihood. We offer an efficient implementation wherein we develop new algorithms for listing, counting, uniformly sampling, and applying possible moves of the GES operators, all of which significantly improve upon the state-of-the-art.

Practical Algorithms for Orientations of Partially Directed Graphical Models

In observational studies, the true causal model is typically unknown and needs to be estimated from available observational and limited experimental data. In such cases, the learned causal model is commonly represented as a partially directed acyclic graph (PDAG), which contains both directed and undirected edges indicating uncertainty of causal relations between random variables. The main focus of this paper is on the maximal orientation task, which, for a given PDAG, aims to orient the undirected edges maximally such that the resulting graph represents the same Markov equivalent DAGs as the input PDAG. This task is a subroutine used frequently in causal discovery, e. g., as the final step of the celebrated PC algorithm. Utilizing connections to the problem of finding a consistent DAG extension of a PDAG, we derive faster algorithms for computing the maximal orientation by proposing two novel approaches for extending PDAGs, both constructed with an emphasis on simplicity and practical effectiveness.

Efficient Enumeration of Markov Equivalent DAGs

Enumerating the directed acyclic graphs (DAGs) of a Markov equivalence class (MEC) is an important primitive in causal analysis. The central resource from the perspective of computational complexity is the delay, that is, the time an algorithm that lists all members of the class requires between two consecutive outputs. Commonly used algorithms for this task utilize the rules proposed by Meek (1995) or the transformational characterization by Chickering (1995), both resulting in superlinear delay. In this paper, we present the first linear-time delay algorithm. On the theoretical side, we show that our algorithm can be generalized to enumerate DAGs represented by models that incorporate background knowledge, such as MPDAGs; on the practical side, we provide an efficient implementation and evaluate it in a series of experiments. Complementary to the linear-time delay algorithm, we also provide intriguing insights into Markov equivalence itself: All members of an MEC can be enumerated such that two successive DAGs have structural Hamming distance at most three.

Finding Front-Door Adjustment Sets in Linear Time

Front-door adjustment is a classic technique to estimate causal effects from a specified directed acyclic graph (DAG) and observed data. The advantage of this approach is that it uses observed mediators to identify causal effects, which is possible even in the presence of unobserved confounding. While the statistical properties of the front-door estimation are quite well understood, its algorithmic aspects remained unexplored for a long time. Recently, Jeong, Tian, and Barenboim [NeurIPS 2022] have presented the first polynomial-time algorithm for finding sets satisfying the front-door criterion in a given DAG, with an $O(n^3(n+m))$ run time, where $n$ denotes the number of variables and $m$ the number of edges of the graph. In our work, we give the first linear-time, i.e. $O(n+m)$, algorithm for this task, which thus reaches the asymptotically optimal time complexity, as the size of the input is $\Omega(n+m)$. We also provide an algorithm to enumerate all front-door adjustment sets in a given DAG with delay $O(n(n + m))$. These results improve the algorithms by Jeong et al. [2022] for the two tasks by a factor of $n^3$, respectively.

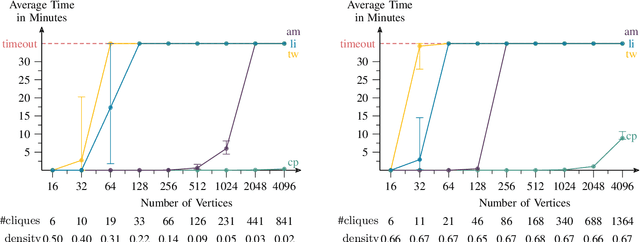
Polynomial-Time Algorithms for Counting and Sampling Markov Equivalent DAGs with Applications

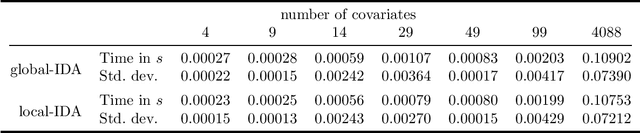
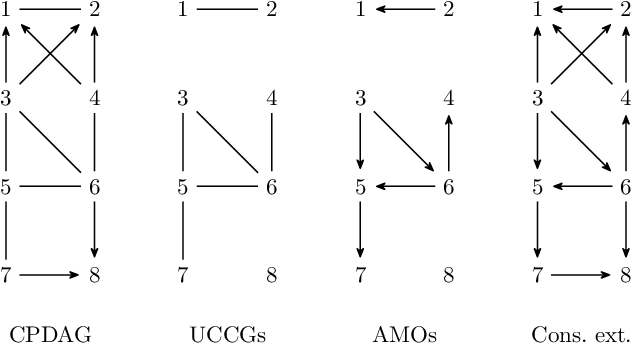
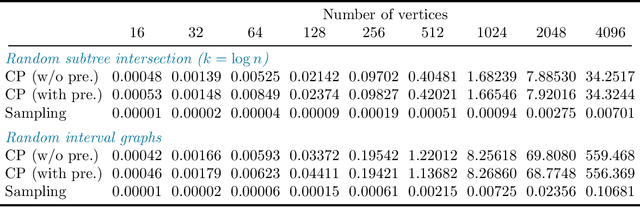
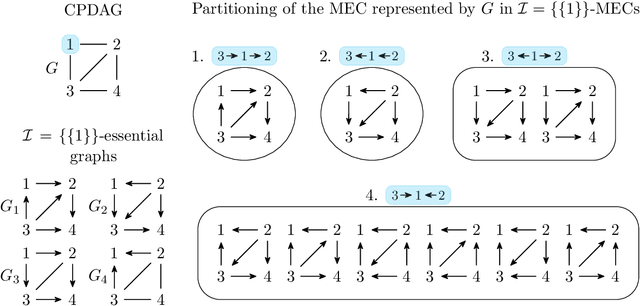
Counting and sampling directed acyclic graphs from a Markov equivalence class are fundamental tasks in graphical causal analysis. In this paper we show that these tasks can be performed in polynomial time, solving a long-standing open problem in this area. Our algorithms are effective and easily implementable. As we show in experiments, these breakthroughs make thought-to-be-infeasible strategies in active learning of causal structures and causal effect identification with regard to a Markov equivalence class practically applicable.

Identification in Tree-shaped Linear Structural Causal Models

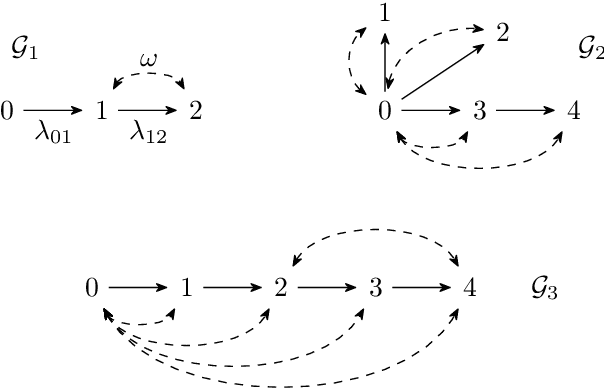
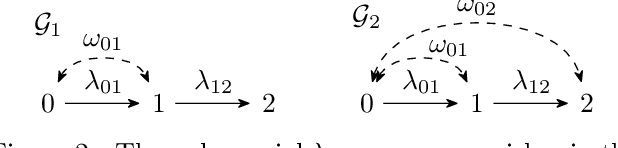
Linear structural equation models represent direct causal effects as directed edges and confounding factors as bidirected edges. An open problem is to identify the causal parameters from correlations between the nodes. We investigate models, whose directed component forms a tree, and show that there, besides classical instrumental variables, missing cycles of bidirected edges can be used to identify the model. They can yield systems of quadratic equations that we explicitly solve to obtain one or two solutions for the causal parameters of adjacent directed edges. We show how multiple missing cycles can be combined to obtain a unique solution. This results in an algorithm that can identify instances that previously required approaches based on Gr\"obner bases, which have doubly-exponential time complexity in the number of structural parameters.

Polynomial-Time Algorithms for Counting and Sampling Markov Equivalent DAGs

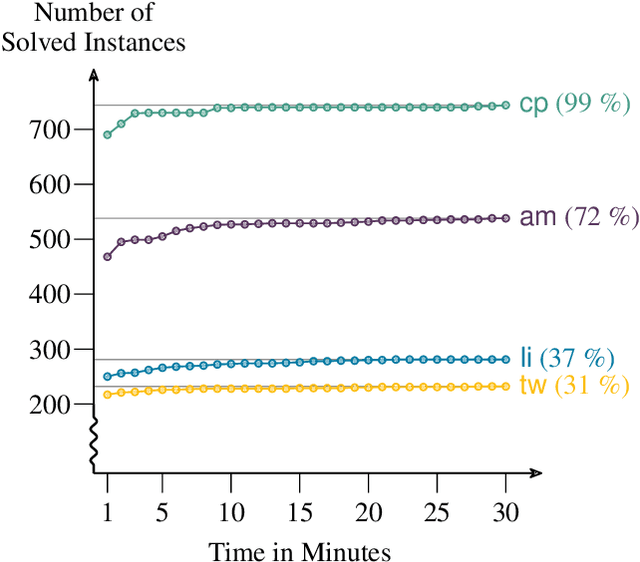
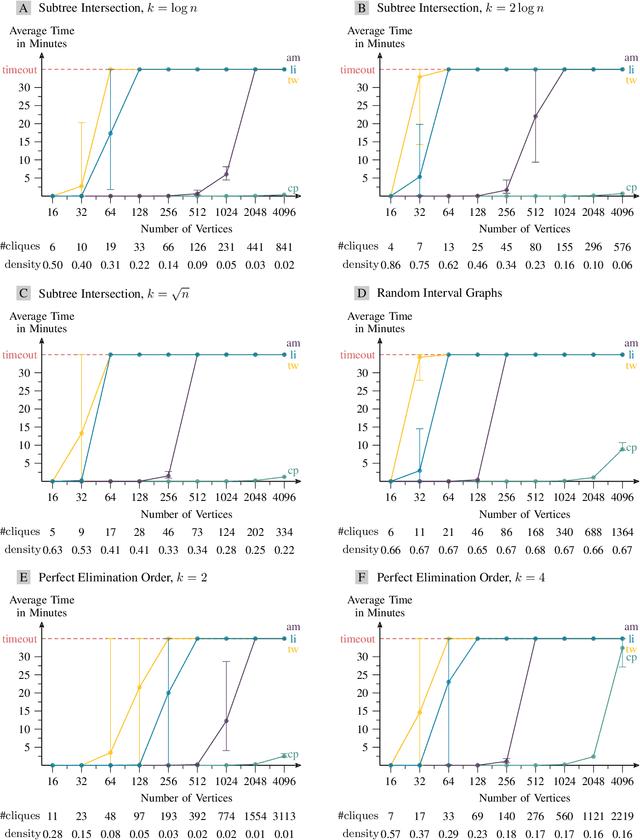
Counting and uniform sampling of directed acyclic graphs (DAGs) from a Markov equivalence class are fundamental tasks in graphical causal analysis. In this paper, we show that these tasks can be performed in polynomial time, solving a long-standing open problem in this area. Our algorithms are effective and easily implementable. Experimental results show that the algorithms significantly outperform state-of-the-art methods.

Recovering Causal Structures from Low-Order Conditional Independencies

One of the common obstacles for learning causal models from data is that high-order conditional independence (CI) relationships between random variables are difficult to estimate. Since CI tests with conditioning sets of low order can be performed accurately even for a small number of observations, a reasonable approach to determine casual structures is to base merely on the low-order CIs. Recent research has confirmed that, e.g. in the case of sparse true causal models, structures learned even from zero- and first-order conditional independencies yield good approximations of the models. However, a challenging task here is to provide methods that faithfully explain a given set of low-order CIs. In this paper, we propose an algorithm which, for a given set of conditional independencies of order less or equal to $k$, where $k$ is a small fixed number, computes a faithful graphical representation of the given set. Our results complete and generalize the previous work on learning from pairwise marginal independencies. Moreover, they enable to improve upon the 0-1 graph model which, e.g. is heavily used in the estimation of genome networks.