Probabilistic and Causal Satisfiability: Constraining the Model

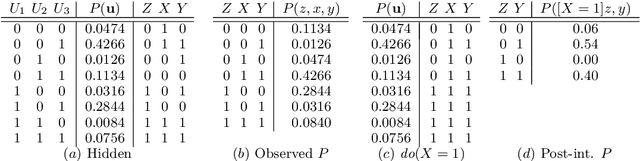
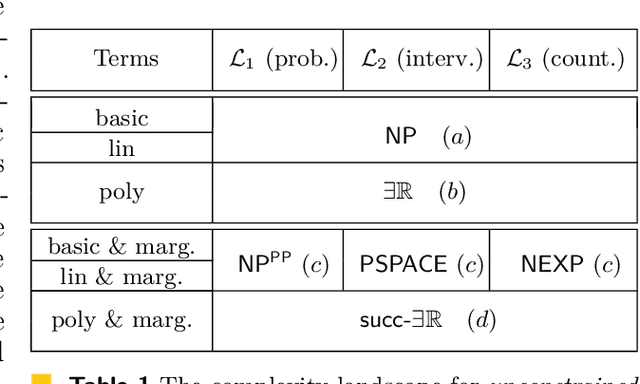
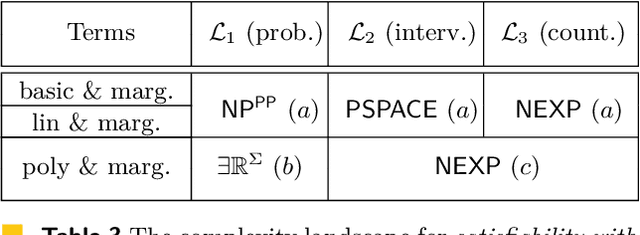
We study the complexity of satisfiability problems in probabilistic and causal reasoning. Given random variables $X_1, X_2,\ldots$ over finite domains, the basic terms are probabilities of propositional formulas over atomic events $X_i = x_i$, such as $P(X_1 = x_1)$ or $P(X_1 = x_1 \vee X_2 = x_2)$. The basic terms can be combined using addition (yielding linear terms) or multiplication (polynomial terms). The probabilistic satisfiability problem asks whether a joint probability distribution satisfies a Boolean combination of (in)equalities over such terms. Fagin et al. (1990) showed that for basic and linear terms, this problem is NP-complete, making it no harder than Boolean satisfiability, while Moss\'e et al. (2022) proved that for polynomial terms, it is complete for the existential theory of the reals. Pearl's Causal Hierarchy (PCH) extends the probabilistic setting with interventional and counterfactual reasoning, enriching the expressiveness of languages. However, Moss\'e et al. (2022) found that satisfiability complexity remains unchanged. Van der Zander et al. (2023) showed that introducing a marginalization operator to languages induces a significant increase in complexity. We extend this line of work by adding two new dimensions to the problem by constraining the models. First, we fix the graph structure of the underlying structural causal model, motivated by settings like Pearl's do-calculus, and give a nearly complete landscape across different arithmetics and PCH levels. Second, we study small models. While earlier work showed that satisfiable instances admit polynomial-size models, this is no longer guaranteed with compact marginalization. We characterize the complexities of satisfiability under small-model constraints across different settings.

On the Complexity of Identification in Linear Structural Causal Models

Learning the unknown causal parameters of a linear structural causal model is a fundamental task in causal analysis. The task, known as the problem of identification, asks to estimate the parameters of the model from a combination of assumptions on the graphical structure of the model and observational data, represented as a non-causal covariance matrix. In this paper, we give a new sound and complete algorithm for generic identification which runs in polynomial space. By standard simulation results, this algorithm has exponential running time which vastly improves the state-of-the-art double exponential time method using a Gr\"obner basis approach. The paper also presents evidence that parameter identification is computationally hard in general. In particular, we prove, that the task asking whether, for a given feasible correlation matrix, there are exactly one or two or more parameter sets explaining the observed matrix, is hard for $\forall R$, the co-class of the existential theory of the reals. In particular, this problem is $coNP$-hard. To our best knowledge, this is the first hardness result for some notion of identifiability.

Probabilistic and Causal Satisfiability: the Impact of Marginalization

The framework of Pearl's Causal Hierarchy (PCH) formalizes three types of reasoning: observational, interventional, and counterfactual, that reflect the progressive sophistication of human thought regarding causation. We investigate the computational complexity aspects of reasoning in this framework focusing mainly on satisfiability problems expressed in probabilistic and causal languages across the PCH. That is, given a system of formulas in the standard probabilistic and causal languages, does there exist a model satisfying the formulas? The resulting complexity changes depending on the level of the hierarchy as well as the operators allowed in the formulas (addition, multiplication, or marginalization). We focus on formulas involving marginalization that are widely used in probabilistic and causal inference, but whose complexity issues are still little explored. Our main contribution are the exact computational complexity results showing that linear languages (allowing addition and marginalization) yield NP^PP-, PSPACE-, and NEXP-complete satisfiability problems, depending on the level of the PCH. Moreover, we prove that the problem for the full language (allowing additionally multiplication) is complete for the class succ$\exists$R for languages on the highest, counterfactual level. Previous work has shown that the satisfiability problem is complete for succ$\exists$R on the lower levels leaving the counterfactual case open. Finally, we consider constrained models that are restricted to a small polynomial size. The constraint on the size reduces the complexity of the interventional and counterfactual languages to NEXP-complete.

Identification for Tree-shaped Structural Causal Models in Polynomial Time

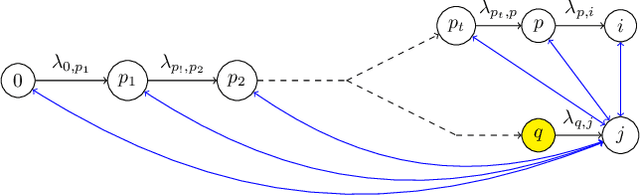
Linear structural causal models (SCMs) are used to express and analyse the relationships between random variables. Direct causal effects are represented as directed edges and confounding factors as bidirected edges. Identifying the causal parameters from correlations between the nodes is an open problem in artificial intelligence. In this paper, we study SCMs whose directed component forms a tree. Van der Zander et al. (AISTATS'22, PLMR 151, pp. 6770--6792, 2022) give a PSPACE-algorithm for the identification problem in this case, which is a significant improvement over the general Gr\"obner basis approach, which has doubly-exponential time complexity in the number of structural parameters. In this work, we present a randomized polynomial-time algorithm, which solves the identification problem for tree-shaped SCMs. For every structural parameter, our algorithms decides whether it is generically identifiable, generically 2-identifiable, or generically unidentifiable. (No other cases can occur.) In the first two cases, it provides one or two fractional affine square root terms of polynomials (FASTPs) for the corresponding parameter, respectively.

The Hardness of Reasoning about Probabilities and Causality

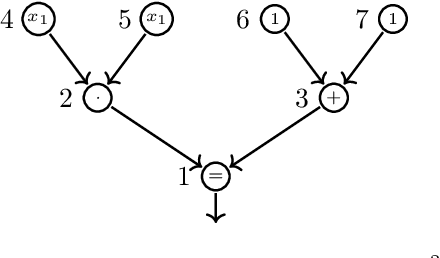
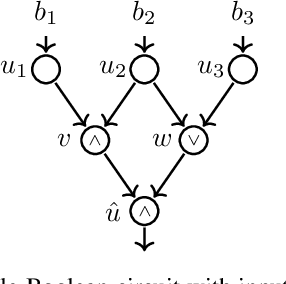
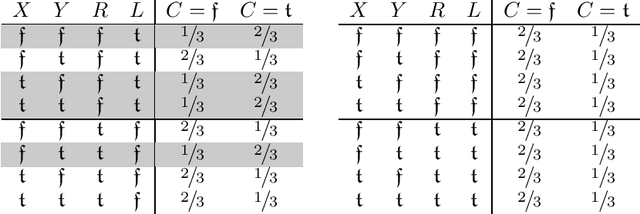
We study formal languages which are capable of fully expressing quantitative probabilistic reasoning and do-calculus reasoning for causal effects, from a computational complexity perspective. We focus on satisfiability problems whose instance formulas allow expressing many tasks in probabilistic and causal inference. The main contribution of this work is establishing the exact computational complexity of these satisfiability problems. We introduce a new natural complexity class, named succ$\exists$R, which can be viewed as a succinct variant of the well-studied class $\exists$R, and show that the problems we consider are complete for succ$\exists$R. Our results imply even stronger algorithmic limitations than were proven by Fagin, Halpern, and Megiddo (1990) and Moss\'{e}, Ibeling, and Icard (2022) for some variants of the standard languages used commonly in probabilistic and causal inference.

Identification in Tree-shaped Linear Structural Causal Models

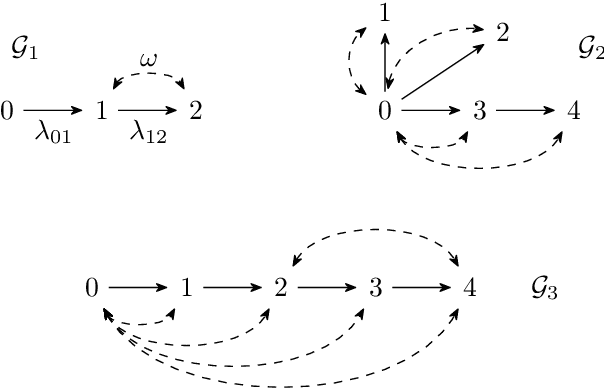
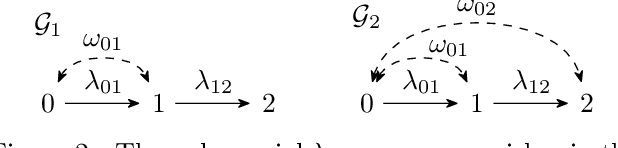
Linear structural equation models represent direct causal effects as directed edges and confounding factors as bidirected edges. An open problem is to identify the causal parameters from correlations between the nodes. We investigate models, whose directed component forms a tree, and show that there, besides classical instrumental variables, missing cycles of bidirected edges can be used to identify the model. They can yield systems of quadratic equations that we explicitly solve to obtain one or two solutions for the causal parameters of adjacent directed edges. We show how multiple missing cycles can be combined to obtain a unique solution. This results in an algorithm that can identify instances that previously required approaches based on Gr\"obner bases, which have doubly-exponential time complexity in the number of structural parameters.