Identification for Tree-shaped Structural Causal Models in Polynomial Time

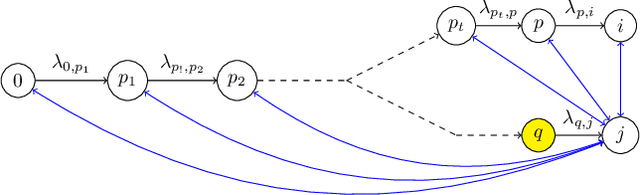
Linear structural causal models (SCMs) are used to express and analyse the relationships between random variables. Direct causal effects are represented as directed edges and confounding factors as bidirected edges. Identifying the causal parameters from correlations between the nodes is an open problem in artificial intelligence. In this paper, we study SCMs whose directed component forms a tree. Van der Zander et al. (AISTATS'22, PLMR 151, pp. 6770--6792, 2022) give a PSPACE-algorithm for the identification problem in this case, which is a significant improvement over the general Gr\"obner basis approach, which has doubly-exponential time complexity in the number of structural parameters. In this work, we present a randomized polynomial-time algorithm, which solves the identification problem for tree-shaped SCMs. For every structural parameter, our algorithms decides whether it is generically identifiable, generically 2-identifiable, or generically unidentifiable. (No other cases can occur.) In the first two cases, it provides one or two fractional affine square root terms of polynomials (FASTPs) for the corresponding parameter, respectively.