Parallel transport on matrix manifolds and Exponential Action
Paper and Code
Aug 12, 2024
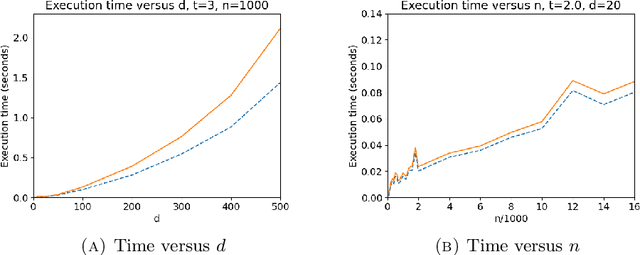
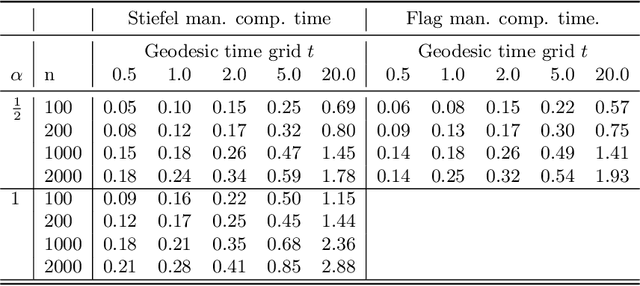
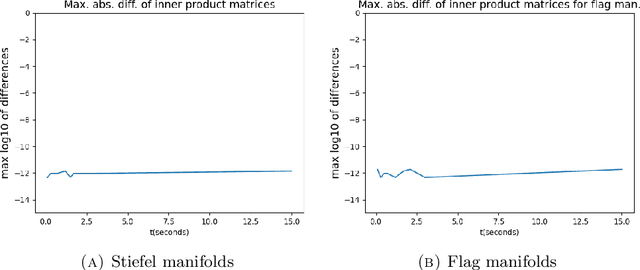
We express parallel transport for several common matrix Lie groups with a family of pseudo-Riemannian metrics in terms of matrix exponential and exponential actions. The expression for parallel transport is preserved by taking the quotient under certain scenarios. In particular, for a Stiefel manifold of orthogonal matrices of size $n\times d$, we give an expression for parallel transport along a geodesic from time zero to $t$, that could be computed with time complexity of $O(nd^2)$ for small $t$, and of $O(td^3)$ for large t, contributing a step in a long-standing open problem in matrix manifolds. A similar result holds for flag manifolds with the canonical metric. We also show the parallel transport formulas for the generalized linear group, and the special orthogonal group under these metrics.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge