Parallel transport on matrix manifolds and Exponential Action

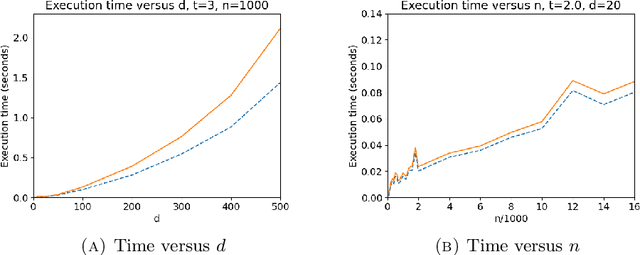
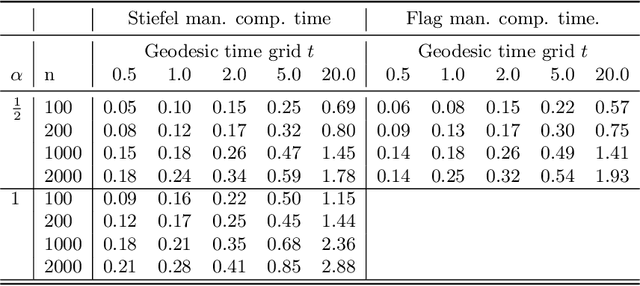
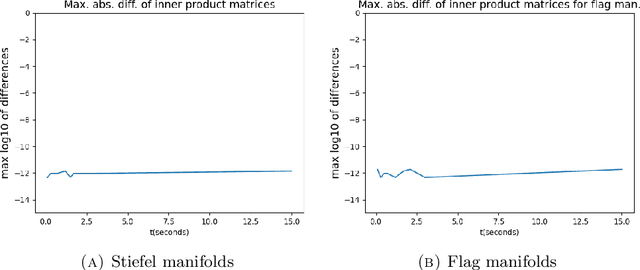
We express parallel transport for several common matrix Lie groups with a family of pseudo-Riemannian metrics in terms of matrix exponential and exponential actions. The expression for parallel transport is preserved by taking the quotient under certain scenarios. In particular, for a Stiefel manifold of orthogonal matrices of size $n\times d$, we give an expression for parallel transport along a geodesic from time zero to $t$, that could be computed with time complexity of $O(nd^2)$ for small $t$, and of $O(td^3)$ for large t, contributing a step in a long-standing open problem in matrix manifolds. A similar result holds for flag manifolds with the canonical metric. We also show the parallel transport formulas for the generalized linear group, and the special orthogonal group under these metrics.

Second-order differential operators, stochastic differential equations and Brownian motions on embedded manifolds

We specify the conditions when a manifold M embedded in an inner product space E is an invariant manifold of a stochastic differential equation (SDE) on E, linking it with the notion of second-order differential operators on M. When M is given a Riemannian metric, we derive a simple formula for the Laplace-Beltrami operator in terms of the gradient and Hessian on E and construct the Riemannian Brownian motions on M as solutions of conservative Stratonovich and Ito SDEs on E. We derive explicitly the SDE for Brownian motions on several important manifolds in applications, including left-invariant matrix Lie groups using embedded coordinates. Numerically, we propose three simulation schemes to solve SDEs on manifolds. In addition to the stochastic projection method, to simulate Riemannian Brownian motions, we construct a second-order tangent retraction of the Levi-Civita connection using a given E-tubular retraction. We also propose the retractive Euler-Maruyama method to solve a SDE, taking into account the second-order term of a tangent retraction. We provide software to implement the methods in the paper, including Brownian motions of the manifolds discussed. We verify numerically that on several compact Riemannian manifolds, the long-term limit of Brownian simulation converges to the uniform distributions, suggesting a method to sample Riemannian uniform distributions

Families of costs with zero and nonnegative MTW tensor in optimal transport

We compute explicitly the MTW tensor (or cross curvature) for the optimal transport problem on $\mathbb{R}^n$ with a cost function of form $\mathsf{c}(x, y) = \mathsf{u}(x^{\mathfrak{t}}y)$, where $\mathsf{u}$ is a scalar function with inverse $\mathsf{s}$, $x^{\ft}y$ is a nondegenerate bilinear pairing of vectors $x, y$ belonging to an open subset of $\mathbb{R}^n$. The condition that the MTW-tensor vanishes on null vectors under the Kim-McCann metric is a fourth-order nonlinear ODE, which could be reduced to a linear ODE of the form $\mathsf{s}^{(2)} - S\mathsf{s}^{(1)} + P\mathsf{s} = 0$ with constant coefficients $P$ and $S$. The resulting inverse functions include {\it Lambert} and {\it generalized inverse hyperbolic\slash trigonometric} functions. The square Euclidean metric and $\log$-type costs are equivalent to instances of these solutions. The optimal map for the family is also explicit. For cost functions of a similar form on a hyperboloid model of the hyperbolic space and unit sphere, we also express this tensor in terms of algebraic expressions in derivatives of $\mathsf{s}$ using the Gauss-Codazzi equation, obtaining new families of strictly regular costs for these manifolds, including new families of {\it power function costs}. We analyze the $\sinh$-type hyperbolic cost, providing examples of $\mathsf{c}$-convex functions and divergence.

Geometry in global coordinates in mechanics and optimal transport

For a manifold embedded in an inner product space, we express geometric quantities such as {\it Hamilton vector fields, affine and Levi-Civita connections, curvature} in global coordinates. Instead of coordinate indices, the global formulas for most quantities are expressed as {\it operator-valued} expressions, using an {\it affine projection} to the tangent bundle. For a submersion image of an embedded manifold, we introduce {\it liftings} of Hamilton vector fields, allowing us to use embedded coordinates on horizontal bundles. We derive a {\it Gauss-Codazzi equation} for affine connections on vector bundles. This approach allows us to evaluate geometric expressions globally, and could be used effectively with modern numerical frameworks in applications. Examples considered include rigid body mechanics and Hamilton mechanics on Grassmann manifolds. We show explicitly the cross-curvature (MTW-tensor) for the {\it Kim-McCann} metric with a reflector antenna-type cost function on the space of positive-semidefinite matrices of fixed rank has nonnegative cross-curvature, while the corresponding cost could have negative cross-curvature on Grassmann manifolds, except for projective spaces.

Road Damages Detection and Classification with YOLOv7

Maintaining the roadway infrastructure is one of the essential factors in enabling a safe, economic, and sustainable transportation system. Manual roadway damage data collection is laborious and unsafe for humans to perform. This area is poised to benefit from the rapid advance and diffusion of artificial intelligence technologies. Specifically, deep learning advancements enable the detection of road damages automatically from the collected road images. This work proposes to collect and label road damage data using Google Street View and use YOLOv7 (You Only Look Once version 7) together with coordinate attention and related accuracy fine-tuning techniques such as label smoothing and ensemble method to train deep learning models for automatic road damage detection and classification. The proposed approaches are applied to the Crowdsensing-based Road Damage Detection Challenge (CRDDC2022), IEEE BigData 2022. The results show that the data collection from Google Street View is efficient, and the proposed deep learning approach results in F1 scores of 81.7% on the road damage data collected from the United States using Google Street View and 74.1% on all test images of this dataset.

Understanding Public Opinion on Using Hydroxychloroquine for COVID-19 Treatment via Social Media

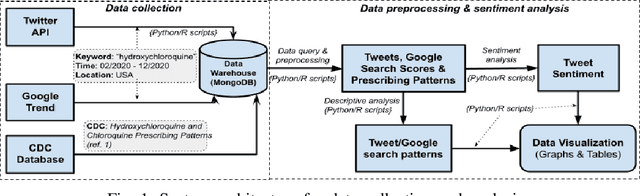
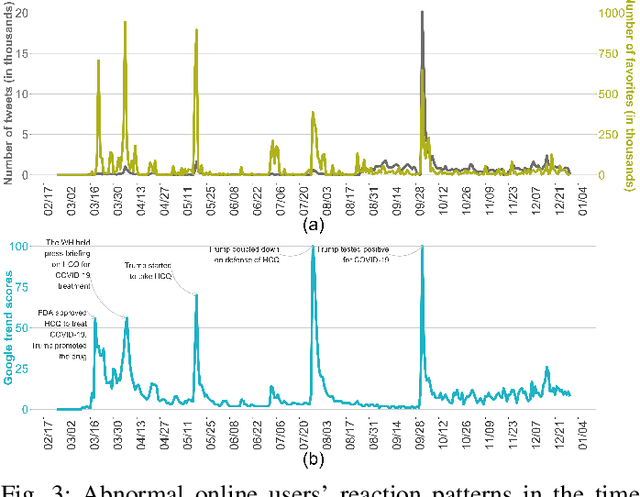
Hydroxychloroquine (HCQ) is used to prevent or treat malaria caused by mosquito bites. Recently, the drug has been suggested to treat COVID-19, but that has not been supported by scientific evidence. The information regarding the drug efficacy has flooded social networks, posting potential threats to the community by perverting their perceptions of the drug efficacy. This paper studies the reactions of social network users on the recommendation of using HCQ for COVID-19 treatment by analyzing the reaction patterns and sentiment of the tweets. We collected 164,016 tweets from February to December 2020 and used a text mining approach to identify social reaction patterns and opinion change over time. Our descriptive analysis identified an irregularity of the users' reaction patterns associated tightly with the social and news feeds on the development of HCQ and COVID-19 treatment. The study linked the tweets and Google search frequencies to reveal the viewpoints of local communities on the use of HCQ for COVID-19 treatment across different states. Further, our tweet sentiment analysis reveals that public opinion changed significantly over time regarding the recommendation of using HCQ for COVID-19 treatment. The data showed that high support in the early dates but it significantly declined in October. Finally, using the manual classification of 4,850 tweets by humans as our benchmark, our sentiment analysis showed that the Google Cloud Natural Language algorithm outperformed the Valence Aware Dictionary and sEntiment Reasoner in classifying tweets, especially in the sarcastic tweet group.

Curvatures of Stiefel manifolds with deformation metrics

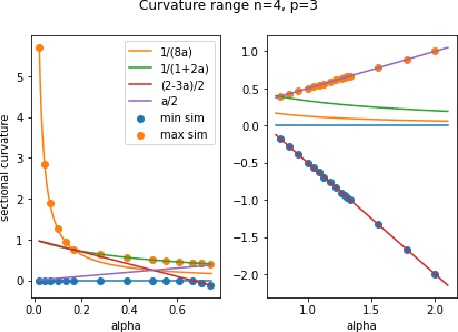
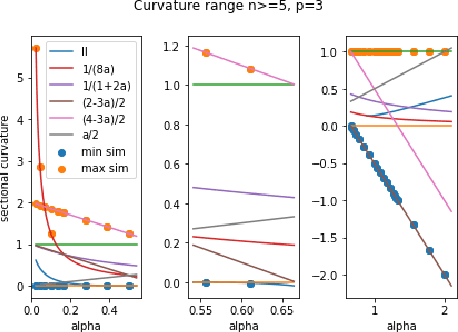
We compute curvatures of a family of tractable metrics on Stiefel manifolds, introduced recently by H{\"u}per, Markina and Silva Leite, which includes the well-known embedded and canonical metrics on Stiefel manifolds as special cases. The metrics could be identified with the Cheeger deformation metrics. We identify parameter values in the family to make a Stiefel manifold an Einstein manifold and show Stiefel manifolds always carry an Einstein metric. We analyze the sectional curvature range and identify the parameter range where the manifold has non-negative sectional curvature. We provide the exact sectional curvature range when the number of columns in a Stiefel matrix is $2$, and a conjectural range for other cases. We derive the formulas from two approaches, one from a global curvature formula derived in our recent work, another using curvature formulas for left-invariant metrics. The second approach leads to curvature formulas for Cheeger deformation metrics on normal homogeneous spaces.

Riemannian Geometry with differentiable ambient space and metric operator

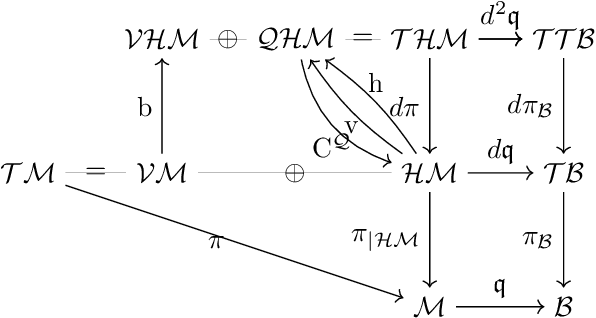
We show Riemannian geometry could be studied by identifying the tangent bundle of a Riemannian manifold $\mathcal{M}$ with a subbundle of the trivial bundle $\mathcal{M} \times \mathcal{E}$, obtained by embedding $\mathcal{M}$ differentiably in a Euclidean space $\mathcal{E}$. Given such an embedding, we can extend the metric tensor on $\mathcal{M}$ to a (positive-definite) operator-valued function acting on $\mathcal{E}$, giving us an embedded ambient structure. The formulas for the Christoffel symbols and Riemannian curvature in local coordinates have simple generalizations to this setup. For a Riemannian submersion $\mathfrak{q}:\mathcal{M}\to \mathcal{B}$ from an embedded manifold $\mathcal{M}\subset \mathcal{E}$, we define a submersed ambient structure and obtain similar formulas, with the O'Neil tensor expressed in terms of the projection to the horizontal bundle $\mathcal{H}\mathcal{M}$. Using this framework, we provide the embedded and submersed ambient structures for the double tangent bundle $\mathcal{T}\mathcal{T}\mathcal{M}$ and the tangent of the horizontal bundle $\mathcal{T}\mathcal{H}\mathcal{M}$, describe the fibration of a horizontal bundle over the tangent bundle of the base manifold and extend the notion of a canonical flip to the submersion case. We obtain a formula for horizontal lifts of Jacobi fields, and a new closed-form formula for Jacobi fields of naturally reductive homogeneous spaces. We construct natural metrics on these double tangent bundles, in particular, extending Sasaki and other natural metrics to the submersion case. We illustrate by providing explicit calculations for several manifolds.

Closed-form geodesics and trust-region method to calculate Riemannian logarithms on Stiefel and its quotient manifolds

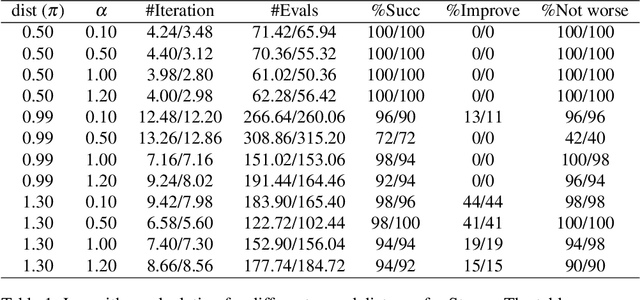
We provide two closed-form geodesic formulas for a family of metrics on Stiefel manifold, parameterized by two positive numbers, having both the embedded and canonical metrics as special cases. The closed-form formulas allow us to compute geodesics by matrix exponential in reduced dimension for low-rank manifolds. Combining with the use of Fr{\'e}chet derivatives to compute the gradient of the square Frobenius distance between a geodesic ending point to a given point on the manifold, we show the logarithm map and geodesic distance between two endpoints on the manifold could be computed by {\it minimizing} this square distance by a {\it trust-region} solver. This leads to a new framework to compute the geodesic distance for manifolds with known geodesic formula but no closed-form logarithm map. We show the approach works well for Stiefel as well as flag manifolds. The logarithm map could be used to compute the Riemannian center of mass for these manifolds equipped with the above metrics. We also deduce simple trigonometric formulas for the Riemannian exponential and logarithm maps on the Grassmann manifold.

Operator-valued formulas for Riemannian Gradient and Hessian and families of tractable metrics in optimization and machine learning

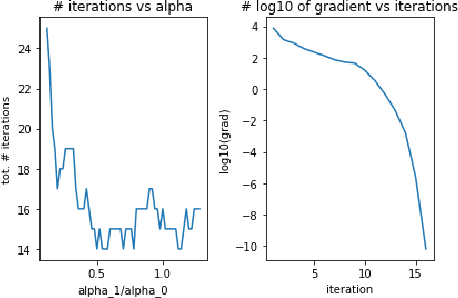
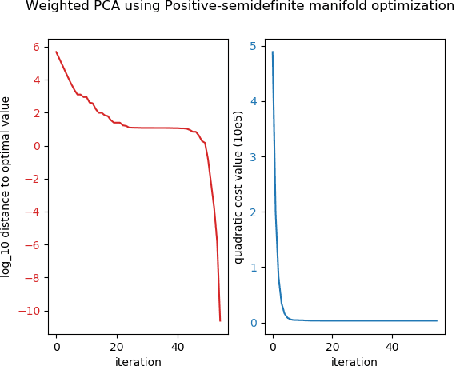
We provide an explicit formula for the Levi-Civita connection and Riemannian Hessian when the {\it tangent space} at each point of a Riemannian manifold is embedded in an inner product space with a non-constant metric. Together with a classical formula for projection, this allows us to evaluate Riemannian gradient and Hessian for several families of metric extending existing ones on classical manifolds: a family of metrics on Stiefel manifolds connecting both the constant and canonical ambient metrics with closed-form geodesics; a family of quotient metrics on a manifold of positive-semidefinite matrices of fixed rank, considered as a quotient of a product of Stiefel and positive-definite matrix manifold with affine-invariant metrics; a large family of new metrics on flag manifolds. We show in many instances, this method allows us to apply symbolic calculus to derive formulas for the Riemannian gradient and Hessian. The method greatly extends the list of potential metrics that could be used in manifold optimization and machine learning.