Closed-form geodesics and trust-region method to calculate Riemannian logarithms on Stiefel and its quotient manifolds
Paper and Code
Mar 12, 2021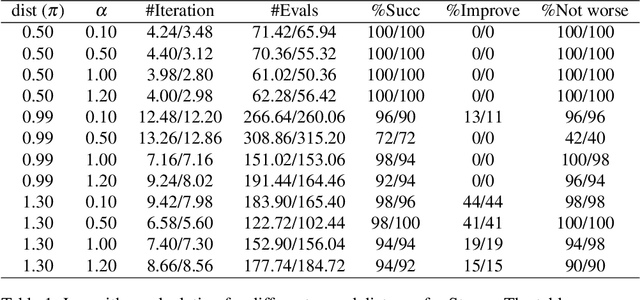



We provide two closed-form geodesic formulas for a family of metrics on Stiefel manifold, parameterized by two positive numbers, having both the embedded and canonical metrics as special cases. The closed-form formulas allow us to compute geodesics by matrix exponential in reduced dimension for low-rank manifolds. Combining with the use of Fr{\'e}chet derivatives to compute the gradient of the square Frobenius distance between a geodesic ending point to a given point on the manifold, we show the logarithm map and geodesic distance between two endpoints on the manifold could be computed by {\it minimizing} this square distance by a {\it trust-region} solver. This leads to a new framework to compute the geodesic distance for manifolds with known geodesic formula but no closed-form logarithm map. We show the approach works well for Stiefel as well as flag manifolds. The logarithm map could be used to compute the Riemannian center of mass for these manifolds equipped with the above metrics. We also deduce simple trigonometric formulas for the Riemannian exponential and logarithm maps on the Grassmann manifold.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge