Riemannian Geometry with differentiable ambient space and metric operator
Paper and Code
May 04, 2021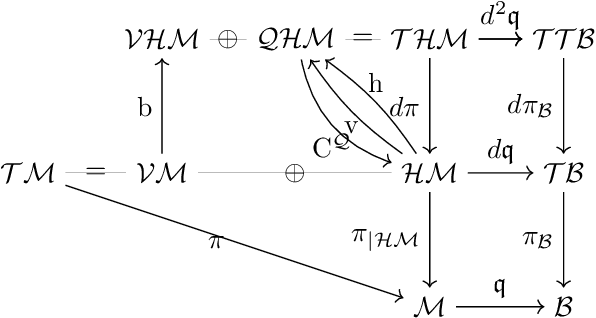
We show Riemannian geometry could be studied by identifying the tangent bundle of a Riemannian manifold $\mathcal{M}$ with a subbundle of the trivial bundle $\mathcal{M} \times \mathcal{E}$, obtained by embedding $\mathcal{M}$ differentiably in a Euclidean space $\mathcal{E}$. Given such an embedding, we can extend the metric tensor on $\mathcal{M}$ to a (positive-definite) operator-valued function acting on $\mathcal{E}$, giving us an embedded ambient structure. The formulas for the Christoffel symbols and Riemannian curvature in local coordinates have simple generalizations to this setup. For a Riemannian submersion $\mathfrak{q}:\mathcal{M}\to \mathcal{B}$ from an embedded manifold $\mathcal{M}\subset \mathcal{E}$, we define a submersed ambient structure and obtain similar formulas, with the O'Neil tensor expressed in terms of the projection to the horizontal bundle $\mathcal{H}\mathcal{M}$. Using this framework, we provide the embedded and submersed ambient structures for the double tangent bundle $\mathcal{T}\mathcal{T}\mathcal{M}$ and the tangent of the horizontal bundle $\mathcal{T}\mathcal{H}\mathcal{M}$, describe the fibration of a horizontal bundle over the tangent bundle of the base manifold and extend the notion of a canonical flip to the submersion case. We obtain a formula for horizontal lifts of Jacobi fields, and a new closed-form formula for Jacobi fields of naturally reductive homogeneous spaces. We construct natural metrics on these double tangent bundles, in particular, extending Sasaki and other natural metrics to the submersion case. We illustrate by providing explicit calculations for several manifolds.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge