Curvatures of Stiefel manifolds with deformation metrics
Paper and Code
May 05, 2021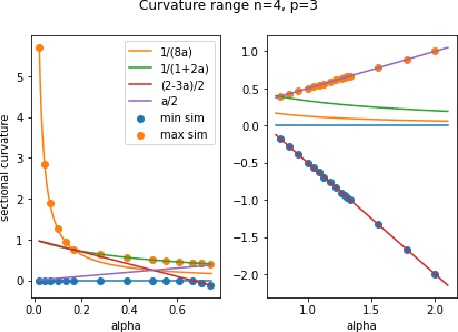
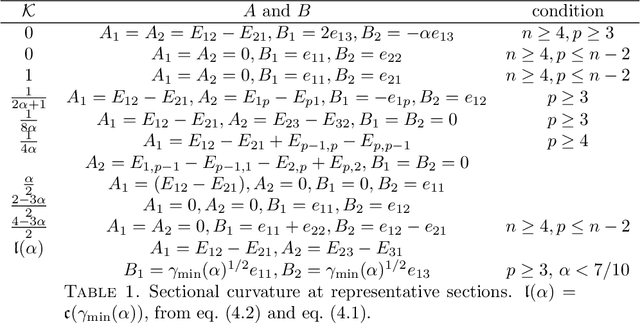
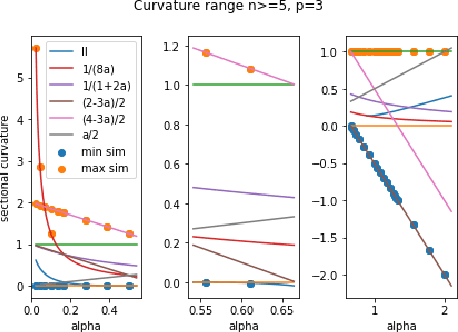

We compute curvatures of a family of tractable metrics on Stiefel manifolds, introduced recently by H{\"u}per, Markina and Silva Leite, which includes the well-known embedded and canonical metrics on Stiefel manifolds as special cases. The metrics could be identified with the Cheeger deformation metrics. We identify parameter values in the family to make a Stiefel manifold an Einstein manifold and show Stiefel manifolds always carry an Einstein metric. We analyze the sectional curvature range and identify the parameter range where the manifold has non-negative sectional curvature. We provide the exact sectional curvature range when the number of columns in a Stiefel matrix is $2$, and a conjectural range for other cases. We derive the formulas from two approaches, one from a global curvature formula derived in our recent work, another using curvature formulas for left-invariant metrics. The second approach leads to curvature formulas for Cheeger deformation metrics on normal homogeneous spaces.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge