Deep Diffeomorphic Normalizing Flows

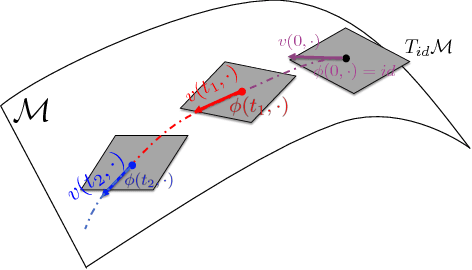
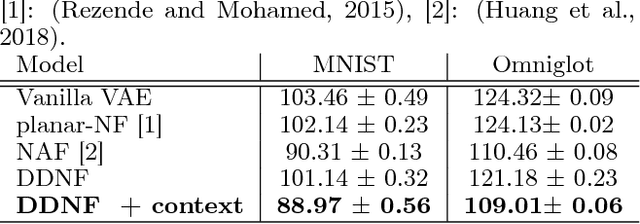
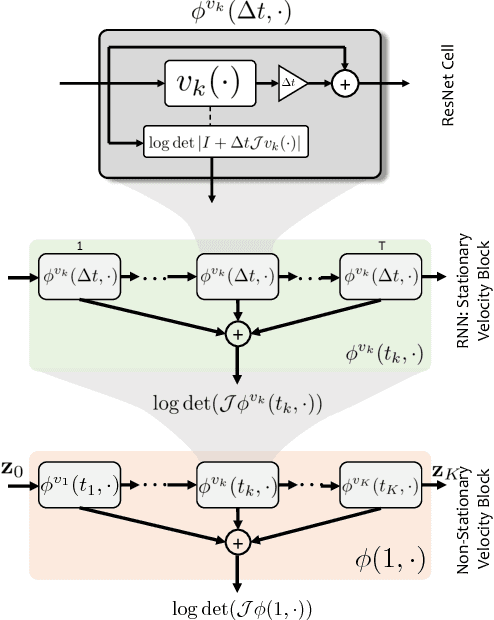
The Normalizing Flow (NF) models a general probability density by estimating an invertible transformation applied on samples drawn from a known distribution. We introduce a new type of NF, called Deep Diffeomorphic Normalizing Flow (DDNF). A diffeomorphic flow is an invertible function where both the function and its inverse are smooth. We construct the flow using an ordinary differential equation (ODE) governed by a time-varying smooth vector field. We use a neural network to parametrize the smooth vector field and a recursive neural network (RNN) for approximating the solution of the ODE. Each cell in the RNN is a residual network implementing one Euler integration step. The architecture of our flow enables efficient likelihood evaluation, straightforward flow inversion, and results in highly flexible density estimation. An end-to-end trained DDNF achieves competitive results with state-of-the-art methods on a suite of density estimation and variational inference tasks. Finally, our method brings concepts from Riemannian geometry that, we believe, can open a new research direction for neural density estimation.

Exploring and Exploiting Diversity for Image Segmentation

Semantic image segmentation is an important computer vision task that is difficult because it consists of both recognition and segmentation. The task is often cast as a structured output problem on an exponentially large output-space, which is typically modeled by a discrete probabilistic model. The best segmentation is found by inferring the Maximum a-Posteriori (MAP) solution over the output distribution defined by the model. Due to limitations in optimization, the model cannot be arbitrarily complex. This leads to a trade-off: devise a more accurate model that incorporates rich high-order interactions between image elements at the cost of inaccurate and possibly intractable optimization OR leverage a tractable model which produces less accurate MAP solutions but may contain high quality solutions as other modes of its output distribution. This thesis investigates the latter and presents a two stage approach to semantic segmentation. In the first stage a tractable segmentation model outputs a set of high probability segmentations from the underlying distribution that are not just minor perturbations of each other. Critically the output of this stage is a diverse set of plausible solutions and not just a single one. In the second stage, a discriminatively trained re-ranking model selects the best segmentation from this set. The re-ranking stage can use much more complex features than what could be tractably used in the segmentation model, allowing a better exploration of the solution space than simply returning the MAP solution. The formulation is agnostic to the underlying segmentation model (e.g. CRF, CNN, etc.) and optimization algorithm, which makes it applicable to a wide range of models and inference methods. Evaluation of the approach on a number of semantic image segmentation benchmark datasets highlight its superiority over inferring the MAP solution.

Feedforward semantic segmentation with zoom-out features

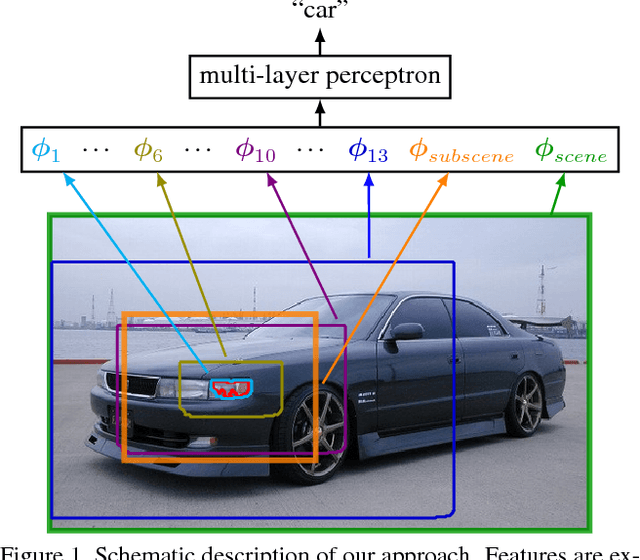
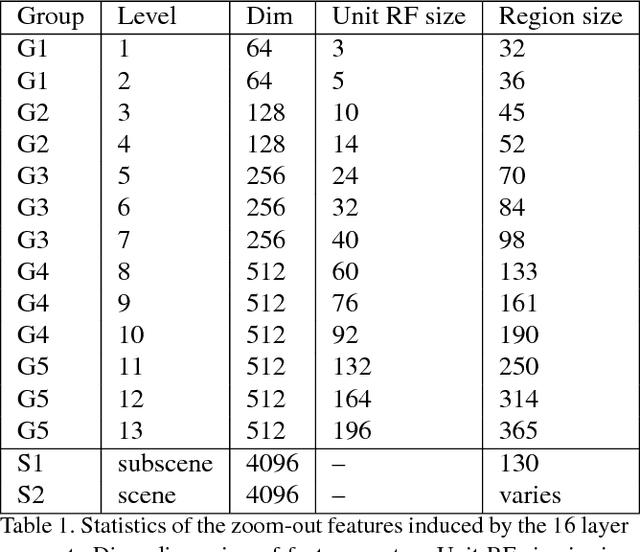
We introduce a purely feed-forward architecture for semantic segmentation. We map small image elements (superpixels) to rich feature representations extracted from a sequence of nested regions of increasing extent. These regions are obtained by "zooming out" from the superpixel all the way to scene-level resolution. This approach exploits statistical structure in the image and in the label space without setting up explicit structured prediction mechanisms, and thus avoids complex and expensive inference. Instead superpixels are classified by a feedforward multilayer network. Our architecture achieves new state of the art performance in semantic segmentation, obtaining 64.4% average accuracy on the PASCAL VOC 2012 test set.

The Power of Asymmetry in Binary Hashing

When approximating binary similarity using the hamming distance between short binary hashes, we show that even if the similarity is symmetric, we can have shorter and more accurate hashes by using two distinct code maps. I.e. by approximating the similarity between $x$ and $x'$ as the hamming distance between $f(x)$ and $g(x')$, for two distinct binary codes $f,g$, rather than as the hamming distance between $f(x)$ and $f(x')$.