Deep Diffeomorphic Normalizing Flows
Paper and Code
Oct 08, 2018
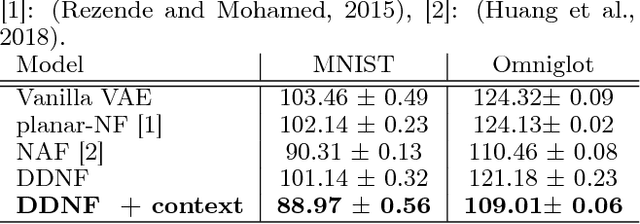
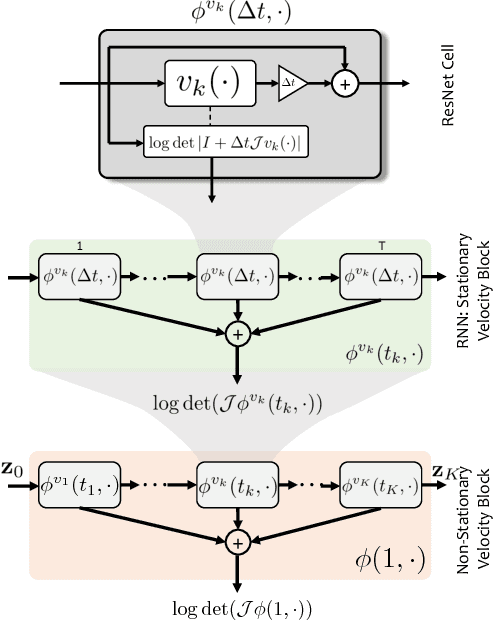

The Normalizing Flow (NF) models a general probability density by estimating an invertible transformation applied on samples drawn from a known distribution. We introduce a new type of NF, called Deep Diffeomorphic Normalizing Flow (DDNF). A diffeomorphic flow is an invertible function where both the function and its inverse are smooth. We construct the flow using an ordinary differential equation (ODE) governed by a time-varying smooth vector field. We use a neural network to parametrize the smooth vector field and a recursive neural network (RNN) for approximating the solution of the ODE. Each cell in the RNN is a residual network implementing one Euler integration step. The architecture of our flow enables efficient likelihood evaluation, straightforward flow inversion, and results in highly flexible density estimation. An end-to-end trained DDNF achieves competitive results with state-of-the-art methods on a suite of density estimation and variational inference tasks. Finally, our method brings concepts from Riemannian geometry that, we believe, can open a new research direction for neural density estimation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge