Line Kuhnel
Latent Space Non-Linear Statistics
May 19, 2018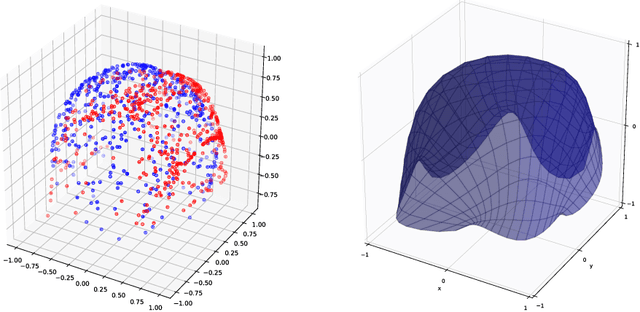
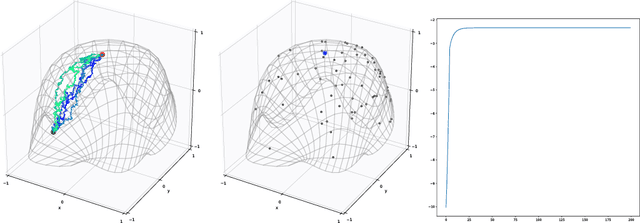
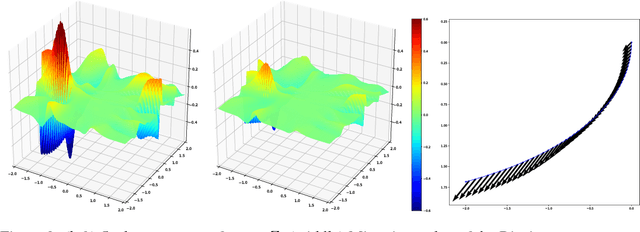
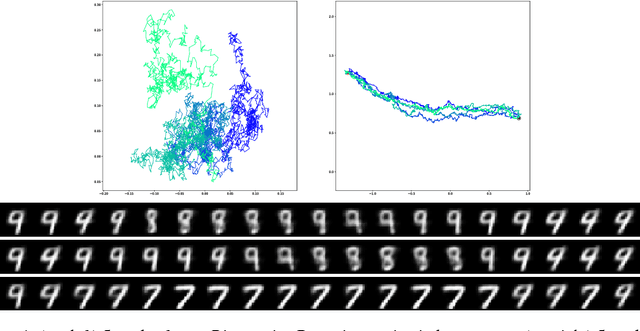
Abstract:Given data, deep generative models, such as variational autoencoders (VAE) and generative adversarial networks (GAN), train a lower dimensional latent representation of the data space. The linear Euclidean geometry of data space pulls back to a nonlinear Riemannian geometry on the latent space. The latent space thus provides a low-dimensional nonlinear representation of data and classical linear statistical techniques are no longer applicable. In this paper we show how statistics of data in their latent space representation can be performed using techniques from the field of nonlinear manifold statistics. Nonlinear manifold statistics provide generalizations of Euclidean statistical notions including means, principal component analysis, and maximum likelihood fits of parametric probability distributions. We develop new techniques for maximum likelihood inference in latent space, and adress the computational complexity of using geometric algorithms with high-dimensional data by training a separate neural network to approximate the Riemannian metric and cometric tensor capturing the shape of the learned data manifold.
Bridge Simulation and Metric Estimation on Landmark Manifolds
May 31, 2017



Abstract:We present an inference algorithm and connected Monte Carlo based estimation procedures for metric estimation from landmark configurations distributed according to the transition distribution of a Riemannian Brownian motion arising from the Large Deformation Diffeomorphic Metric Mapping (LDDMM) metric. The distribution possesses properties similar to the regular Euclidean normal distribution but its transition density is governed by a high-dimensional PDE with no closed-form solution in the nonlinear case. We show how the density can be numerically approximated by Monte Carlo sampling of conditioned Brownian bridges, and we use this to estimate parameters of the LDDMM kernel and thus the metric structure by maximum likelihood.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge