Information-Theoretic Measures on Lattices for High-Order Interactions

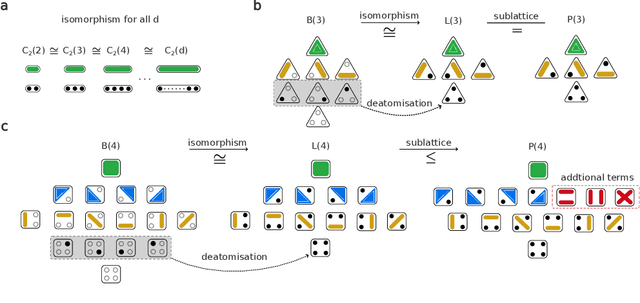
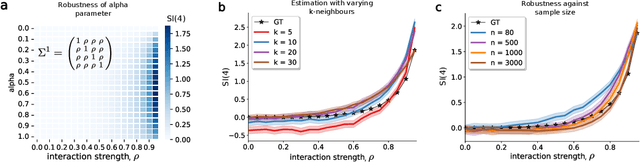
Traditional models reliant solely on pairwise associations often prove insufficient in capturing the complex statistical structure inherent in multivariate data. Yet existing methods for identifying information shared among groups of $d>3$ variables are often intractable; asymmetric around a target variable; or unable to consider all factorisations of the joint probability distribution. Here, we present a framework that systematically derives high-order measures using lattice and operator function pairs, whereby the lattice captures the algebraic relational structure of the variables and the operator function computes measures over the lattice. We show that many existing information-theoretic high-order measures can be derived by using divergences as operator functions on sublattices of the partition lattice, thus preventing the accurate quantification of all interactions for $d>3$. Similarly, we show that using the KL divergence as the operator function also leads to unwanted cancellation of interactions for $d>3$. To characterise all interactions among $d$ variables, we introduce the Streitberg information defined on the full partition lattice using generalisations of the KL divergence as operator functions. We validate our results numerically on synthetic data, and illustrate the use of the Streitberg information through applications to stock market returns and neural electrophysiology data.

Implicit Gaussian process representation of vector fields over arbitrary latent manifolds

Gaussian processes (GPs) are popular nonparametric statistical models for learning unknown functions and quantifying the spatiotemporal uncertainty in data. Recent works have extended GPs to model scalar and vector quantities distributed over non-Euclidean domains, including smooth manifolds appearing in numerous fields such as computer vision, dynamical systems, and neuroscience. However, these approaches assume that the manifold underlying the data is known, limiting their practical utility. We introduce RVGP, a generalisation of GPs for learning vector signals over latent Riemannian manifolds. Our method uses positional encoding with eigenfunctions of the connection Laplacian, associated with the tangent bundle, readily derived from common graph-based approximation of data. We demonstrate that RVGP possesses global regularity over the manifold, which allows it to super-resolve and inpaint vector fields while preserving singularities. Furthermore, we use RVGP to reconstruct high-density neural dynamics derived from low-density EEG recordings in healthy individuals and Alzheimer's patients. We show that vector field singularities are important disease markers and that their reconstruction leads to a comparable classification accuracy of disease states to high-density recordings. Thus, our method overcomes a significant practical limitation in experimental and clinical applications.

Interaction Measures, Partition Lattices and Kernel Tests for High-Order Interactions

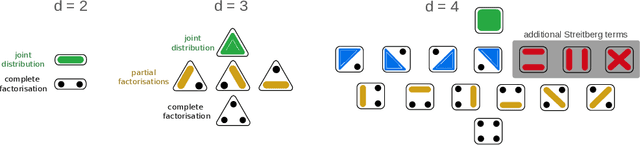
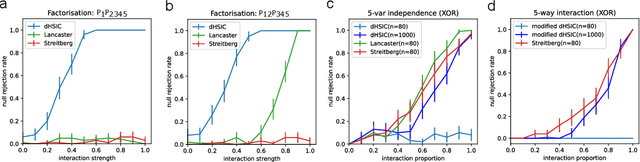
Models that rely solely on pairwise relationships often fail to capture the complete statistical structure of the complex multivariate data found in diverse domains, such as socio-economic, ecological, or biomedical systems. Non-trivial dependencies between groups of more than two variables can play a significant role in the analysis and modelling of such systems, yet extracting such high-order interactions from data remains challenging. Here, we introduce a hierarchy of $d$-order ($d \geq 2$) interaction measures, increasingly inclusive of possible factorisations of the joint probability distribution, and define non-parametric, kernel-based tests to establish systematically the statistical significance of $d$-order interactions. We also establish mathematical links with lattice theory, which elucidate the derivation of the interaction measures and their composite permutation tests; clarify the connection of simplicial complexes with kernel matrix centring; and provide a means to enhance computational efficiency. We illustrate our results numerically with validations on synthetic data, and through an application to neuroimaging data.

Kernel-based Joint Independence Tests for Multivariate Stationary and Nonstationary Time-Series

Multivariate time-series data that capture the temporal evolution of interconnected systems are ubiquitous in diverse areas. Understanding the complex relationships and potential dependencies among co-observed variables is crucial for the accurate statistical modelling and analysis of such systems. Here, we introduce kernel-based statistical tests of joint independence in multivariate time-series by extending the d-variable Hilbert-Schmidt independence criterion (dHSIC) to encompass both stationary and nonstationary random processes, thus allowing broader real-world applications. By leveraging resampling techniques tailored for both single- and multiple-realization time series, we show how the method robustly uncovers significant higher-order dependencies in synthetic examples, including frequency mixing data, as well as real-world climate and socioeconomic data. Our method adds to the mathematical toolbox for the analysis of complex high-dimensional time-series datasets.

Interpretable statistical representations of neural population dynamics and geometry

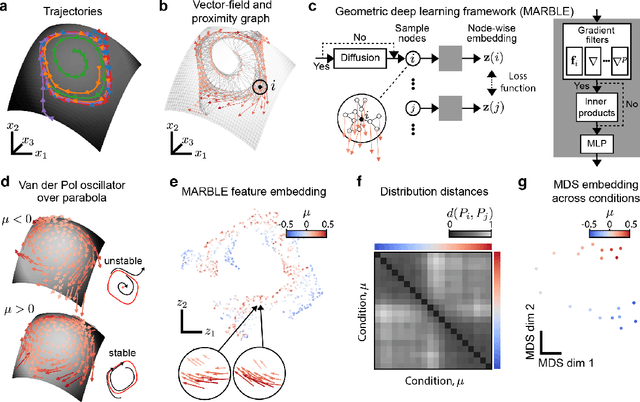
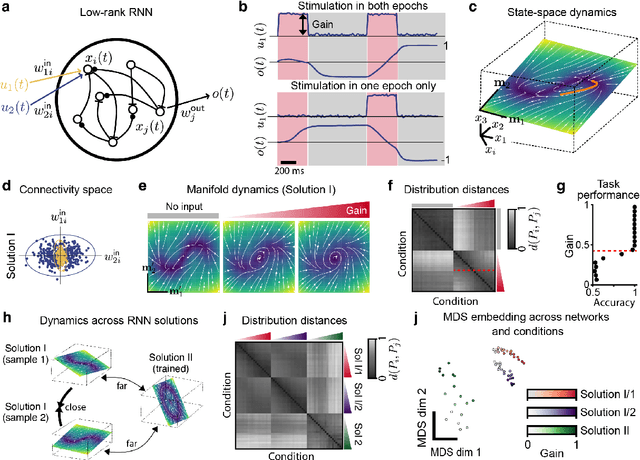
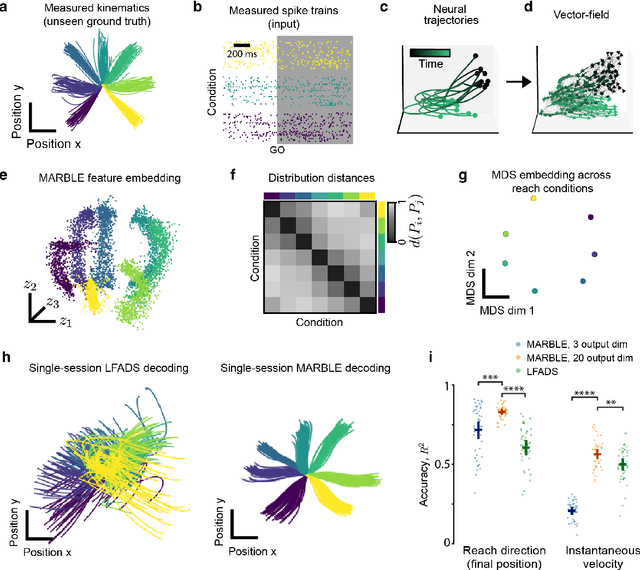
The dynamics of neuron populations during diverse tasks often evolve on low-dimensional manifolds. However, it remains challenging to discern the contributions of geometry and dynamics for encoding relevant behavioural variables. Here, we introduce an unsupervised geometric deep learning framework for representing non-linear dynamical systems based on statistical distributions of local phase portrait features. Our method provides robust geometry-aware or geometry-agnostic representations for the unbiased comparison of dynamics based on measured trajectories. We demonstrate that our statistical representation can generalise across neural network instances to discriminate computational mechanisms, obtain interpretable embeddings of neural dynamics in a primate reaching task with geometric correspondence to hand kinematics, and develop a decoding algorithm with state-of-the-art accuracy. Our results highlight the importance of using the intrinsic manifold structure over temporal information to develop better decoding algorithms and assimilate data across experiments.

Semi-supervised classification on graphs using explicit diffusion dynamics

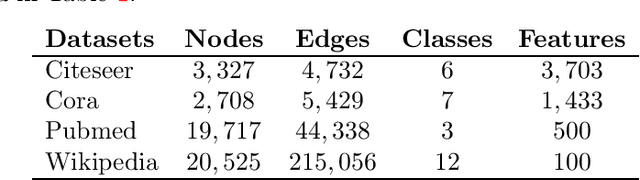
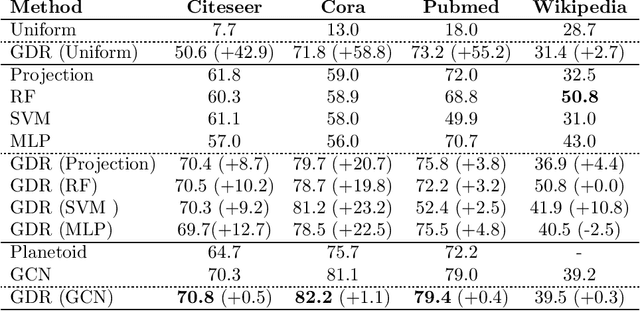
Classification tasks based on feature vectors can be significantly improved by including within deep learning a graph that summarises pairwise relationships between the samples. Intuitively, the graph acts as a conduit to channel and bias the inference of class labels. Here, we study classification methods that consider the graph as the originator of an explicit graph diffusion. We show that appending graph diffusion to feature-based learning as an \textit{a posteriori} refinement achieves state-of-the-art classification accuracy. This method, which we call Graph Diffusion Reclassification (GDR), uses overshooting events of a diffusive graph dynamics to reclassify individual nodes. The method uses intrinsic measures of node influence, which are distinct for each node, and allows the evaluation of the relationship and importance of features and graph for classification. We also present diff-GCN, a simple extension of Graph Convolutional Neural Network (GCN) architectures that leverages explicit diffusion dynamics, and allows the natural use of directed graphs. To showcase our methods, we use benchmark datasets of documents with associated citation data.