Planar Curve Registration using Bayesian Inversion

We study parameterisation-independent closed planar curve matching as a Bayesian inverse problem. The motion of the curve is modelled via a curve on the diffeomorphism group acting on the ambient space, leading to a large deformation diffeomorphic metric mapping (LDDMM) functional penalising the kinetic energy of the deformation. We solve Hamilton's equations for the curve matching problem using the Wu-Xu element [S. Wu, J. Xu, Nonconforming finite element spaces for $2m^\text{th}$ order partial differential equations on $\mathbb{R}^n$ simplicial grids when $m=n+1$, Mathematics of Computation 88 (316) (2019) 531-551] which provides mesh-independent Lipschitz constants for the forward motion of the curve, and solve the inverse problem for the momentum using Bayesian inversion. Since this element is not affine-equivalent we provide a pullback theory which expedites the implementation and efficiency of the forward map. We adopt ensemble Kalman inversion using a negative Sobolev norm mismatch penalty to measure the discrepancy between the target and the ensemble mean shape. We provide several numerical examples to validate the approach.

Learning landmark geodesics using Kalman ensembles

We study the problem of diffeomorphometric geodesic landmark matching where the objective is to find a diffeomorphism that via its group action maps between two sets of landmarks. It is well-known that the motion of the landmarks, and thereby the diffeomorphism, can be encoded by an initial momentum leading to a formulation where the landmark matching problem can be solved as an optimisation problem over such momenta. The novelty of our work lies in the application of a derivative-free Bayesian inverse method for learning the optimal momentum encoding the diffeomorphic mapping between the template and the target. The method we apply is the ensemble Kalman filter, an extension of the Kalman filter to nonlinear observation operators. We describe an efficient implementation of the algorithm and show several numerical results for various target shapes.

Selective metamorphosis for growth modelling with applications to landmarks

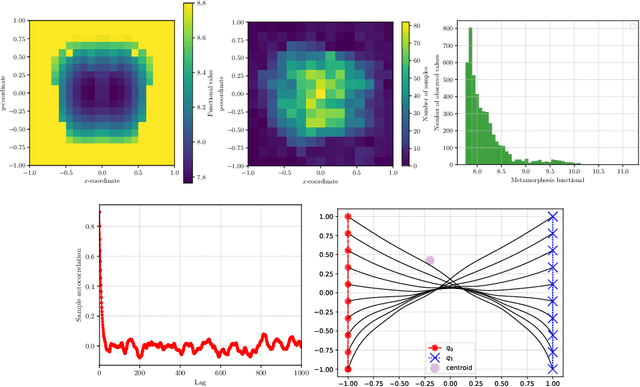
We present a framework for shape matching in computational anatomy allowing users control of the degree to which the matching is diffeomorphic. This control is given as a function defined over the image and parameterises the template deformation. By modelling localised template deformation we have a mathematical description of growth only in specified parts of an image. The location can either be specified from prior knowledge of the growth location or learned from data. For simplicity, we consider landmark matching and infer the distribution of a finite dimensional parameterisation of the control via Markov chain Monte Carlo. Preliminary numerical results are shown and future paths of investigation are laid out. Well-posedness of this new problem is studied together with an analysis of the associated geodesic equations.