Darryl Holm
String Methods for Stochastic Image and Shape Matching
Oct 20, 2018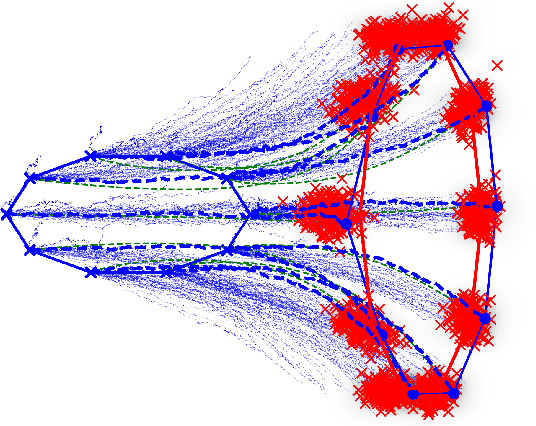
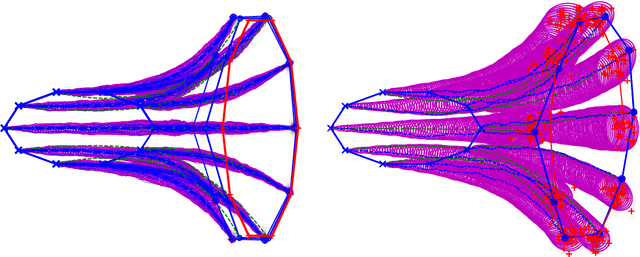
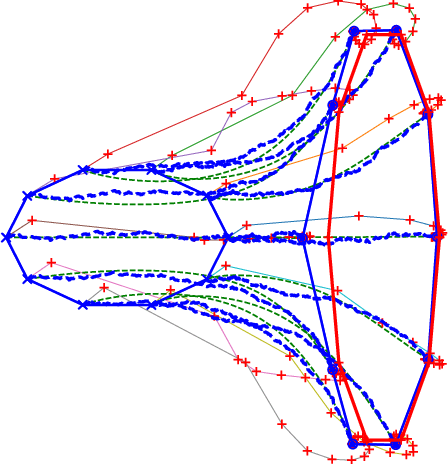

Abstract:Matching of images and analysis of shape differences is traditionally pursued by energy minimization of paths of deformations acting to match the shape objects. In the Large Deformation Diffeomorphic Metric Mapping (LDDMM) framework, iterative gradient descents on the matching functional lead to matching algorithms informally known as Beg algorithms. When stochasticity is introduced to model stochastic variability of shapes and to provide more realistic models of observed shape data, the corresponding matching problem can be solved with a stochastic Beg algorithm, similar to the finite temperature string method used in rare event sampling. In this paper, we apply a stochastic model compatible with the geometry of the LDDMM framework to obtain a stochastic model of images and we derive the stochastic version of the Beg algorithm which we compare with the string method and an expectation-maximization optimization of posterior likelihoods. The algorithm and its use for statistical inference is tested on stochastic LDDMM landmarks and images.
Stochastic metamorphosis with template uncertainties
Nov 20, 2017


Abstract:In this paper, we investigate two stochastic perturbations of the metamorphosis equations of image analysis, in the geometrical context of the Euler-Poincar\'e theory. In the metamorphosis of images, the Lie group of diffeomorphisms deforms a template image that is undergoing its own internal dynamics as it deforms. This type of deformation allows more freedom for image matching and has analogies with complex fluids when the template properties are regarded as order parameters (coset spaces of broken symmetries). The first stochastic perturbation we consider corresponds to uncertainty due to random errors in the reconstruction of the deformation map from its vector field. We also consider a second stochastic perturbation, which compounds the uncertainty in of the deformation map with the uncertainty in the reconstruction of the template position from its velocity field. We apply this general geometric theory to several classical examples, including landmarks, images, and closed curves, and we discuss its use for functional data analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge