A Geometric Framework for Stochastic Shape Analysis

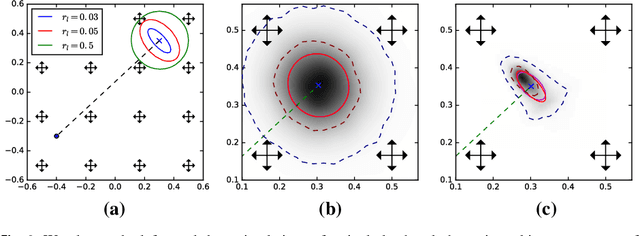
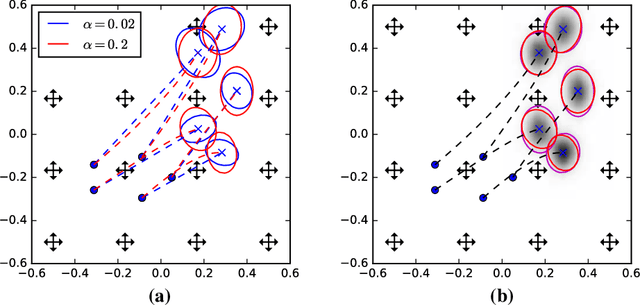
We introduce a stochastic model of diffeomorphisms, whose action on a variety of data types descends to stochastic evolution of shapes, images and landmarks. The stochasticity is introduced in the vector field which transports the data in the Large Deformation Diffeomorphic Metric Mapping (LDDMM) framework for shape analysis and image registration. The stochasticity thereby models errors or uncertainties of the flow in following the prescribed deformation velocity. The approach is illustrated in the example of finite dimensional landmark manifolds, whose stochastic evolution is studied both via the Fokker-Planck equation and by numerical simulations. We derive two approaches for inferring parameters of the stochastic model from landmark configurations observed at discrete time points. The first of the two approaches matches moments of the Fokker-Planck equation to sample moments of the data, while the second approach employs an Expectation-Maximisation based algorithm using a Monte Carlo bridge sampling scheme to optimise the data likelihood. We derive and numerically test the ability of the two approaches to infer the spatial correlation length of the underlying noise.

A Stochastic Large Deformation Model for Computational Anatomy

In the study of shapes of human organs using computational anatomy, variations are found to arise from inter-subject anatomical differences, disease-specific effects, and measurement noise. This paper introduces a stochastic model for incorporating random variations into the Large Deformation Diffeomorphic Metric Mapping (LDDMM) framework. By accounting for randomness in a particular setup which is crafted to fit the geometrical properties of LDDMM, we formulate the template estimation problem for landmarks with noise and give two methods for efficiently estimating the parameters of the noise fields from a prescribed data set. One method directly approximates the time evolution of the variance of each landmark by a finite set of differential equations, and the other is based on an Expectation-Maximisation algorithm. In the second method, the evaluation of the data likelihood is achieved without registering the landmarks, by applying bridge sampling using a stochastically perturbed version of the large deformation gradient flow algorithm. The method and the estimation algorithms are experimentally validated on synthetic examples and shape data of human corpora callosa.

The Euler-Poincare theory of Metamorphosis

In the pattern matching approach to imaging science, the process of ``metamorphosis'' is template matching with dynamical templates. Here, we recast the metamorphosis equations of into the Euler-Poincare variational framework of and show that the metamorphosis equations contain the equations for a perfect complex fluid \cite{Ho2002}. This result connects the ideas underlying the process of metamorphosis in image matching to the physical concept of order parameter in the theory of complex fluids. After developing the general theory, we reinterpret various examples, including point set, image and density metamorphosis. We finally discuss the issue of matching measures with metamorphosis, for which we provide existence theorems for the initial and boundary value problems.