Introduction to Machine Learning

This book introduces the mathematical foundations and techniques that lead to the development and analysis of many of the algorithms that are used in machine learning. It starts with an introductory chapter that describes notation used throughout the book and serve at a reminder of basic concepts in calculus, linear algebra and probability and also introduces some measure theoretic terminology, which can be used as a reading guide for the sections that use these tools. The introductory chapters also provide background material on matrix analysis and optimization. The latter chapter provides theoretical support to many algorithms that are used in the book, including stochastic gradient descent, proximal methods, etc. After discussing basic concepts for statistical prediction, the book includes an introduction to reproducing kernel theory and Hilbert space techniques, which are used in many places, before addressing the description of various algorithms for supervised statistical learning, including linear methods, support vector machines, decision trees, boosting, or neural networks. The subject then switches to generative methods, starting with a chapter that presents sampling methods and an introduction to the theory of Markov chains. The following chapter describe the theory of graphical models, an introduction to variational methods for models with latent variables, and to deep-learning based generative models. The next chapters focus on unsupervised learning methods, for clustering, factor analysis and manifold learning. The final chapter of the book is theory-oriented and discusses concentration inequalities and generalization bounds.

FineMorphs: Affine-diffeomorphic sequences for regression

A multivariate regression model of affine and diffeomorphic transformation sequences - FineMorphs - is presented. Leveraging concepts from shape analysis, model states are optimally "reshaped" by diffeomorphisms generated by smooth vector fields during learning. Affine transformations and vector fields are optimized within an optimal control setting, and the model can naturally reduce (or increase) dimensionality and adapt to large datasets via suboptimal vector fields. An existence proof of solution and necessary conditions for optimality for the model are derived. Experimental results on real datasets from the UCI repository are presented, with favorable results in comparison with state-of-the-art in the literature and densely-connected neural networks in TensorFlow.

A generative neural network model for random dot product graphs

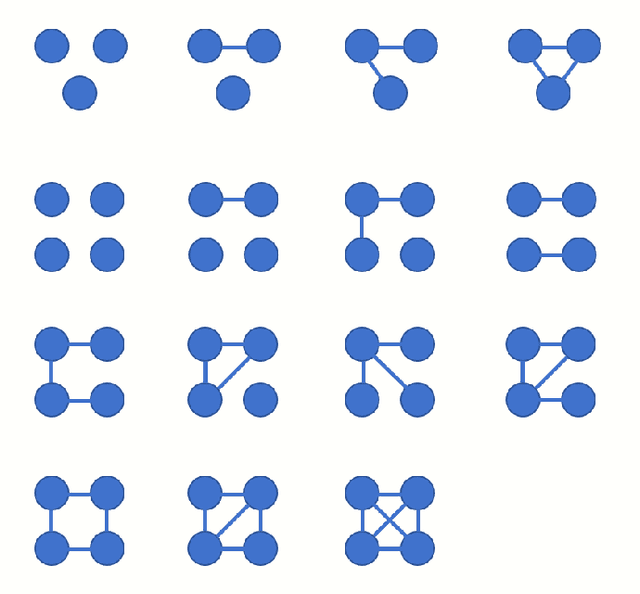
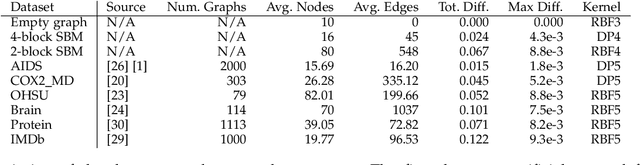
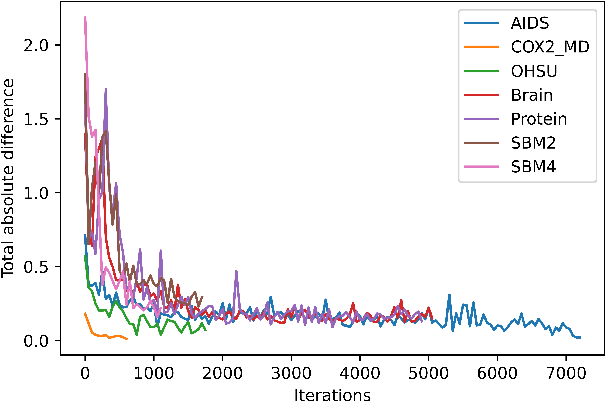
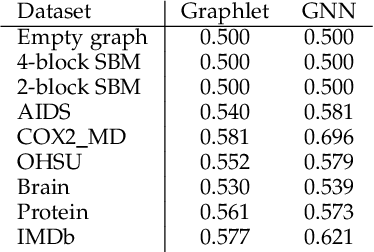
We present GraphMoE, a novel neural network-based approach to learning generative models for random graphs. The neural network is trained to match the distribution of a class of random graphs by way of a moment estimator. The features used for training are graphlets, subgraph counts of small order. The neural network accepts random noise as input and outputs vector representations for nodes in the graph. Random graphs are then realized by applying a kernel to the representations. Graphs produced this way are demonstrated to be able to imitate data from chemistry, medicine, and social networks. The produced graphs are similar enough to the target data to be able to fool discriminator neural networks otherwise capable of separating classes of random graphs.

3D Normal Coordinate Systems for Cortical Areas

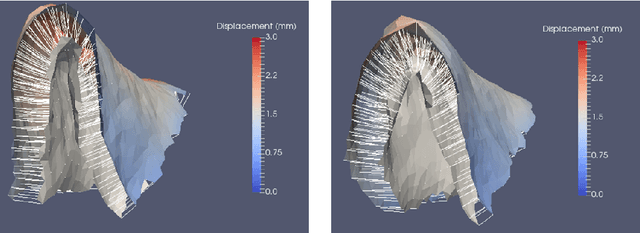
A surface-based diffeomorphic algorithm to generate 3D coordinate grids in the cortical ribbon is described. In the grid, normal coordinate lines are generated by the diffeomorphic evolution from the grey/white (inner) surface to the grey/csf (outer) surface. Specifically, the cortical ribbon is described by two triangulated surfaces with open boundaries. Conceptually, the inner surface sits on top of the white matter structure and the outer on top of the gray matter. It is assumed that the cortical ribbon consists of cortical columns which are orthogonal to the white matter surface. This might be viewed as a consequence of the development of the columns in the embryo. It is also assumed that the columns are orthogonal to the outer surface so that the resultant vector field is orthogonal to the evolving surface. Then the distance of the normal lines from the vector field such that the inner surface evolves diffeomorphically towards the outer one can be construed as a measure of thickness. Applications are described for the auditory cortices in human adults and cats with normal hearing or hearing loss. The approach offers great potential for cortical morphometry.

Diffeomorphic Learning

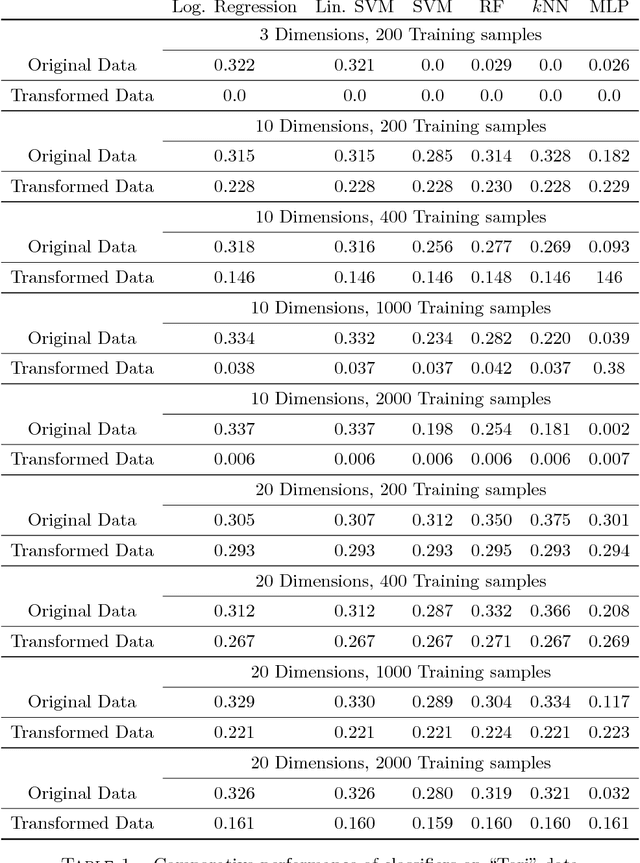
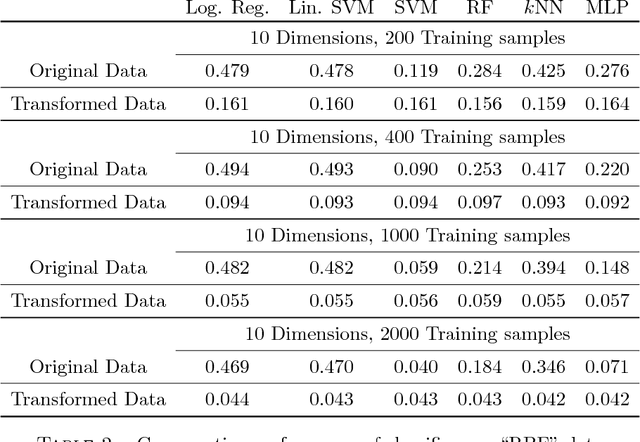
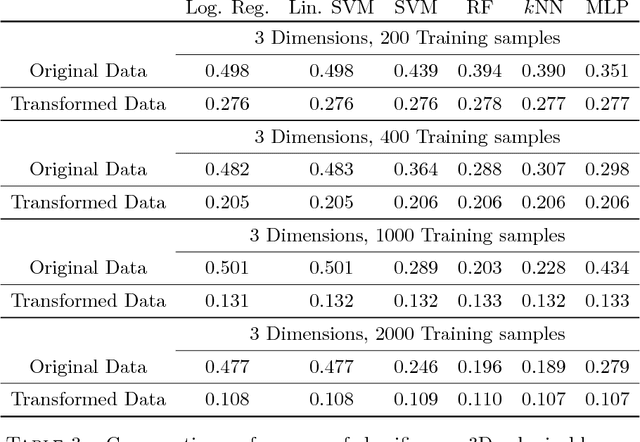
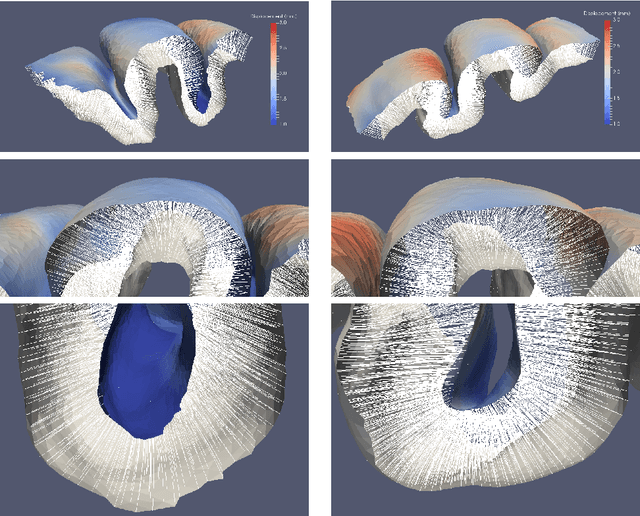
We introduce in this paper a learning paradigm in which the training data is transformed by a diffeomorphic transformation before prediction. The learning algorithm minimizes a cost function evaluating the prediction error on the training set penalized by the distance between the diffeomorphism and the identity. The approach borrows ideas from shape analysis, in the way diffeomorphisms are estimated for shape and image alignment, and brings them in a previously unexplored setting, estimating, in particular diffeomorphisms in much larger dimensions. After introducing the concept and describing a learning algorithm, we present diverse applications, mostly with synthetic examples, demonstrating the potential of the approach, as well as some of its current room for improvement.

Information Pursuit: A Bayesian Framework for Sequential Scene Parsing

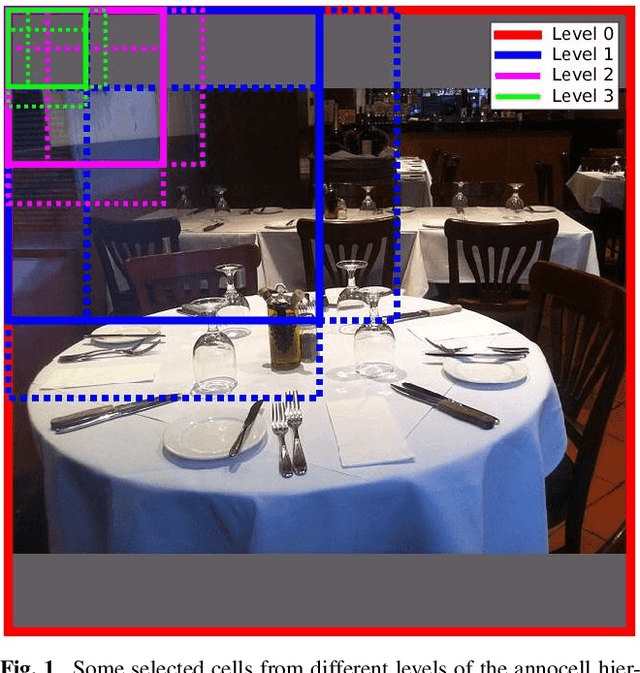
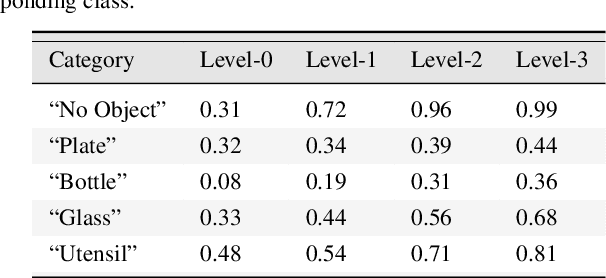
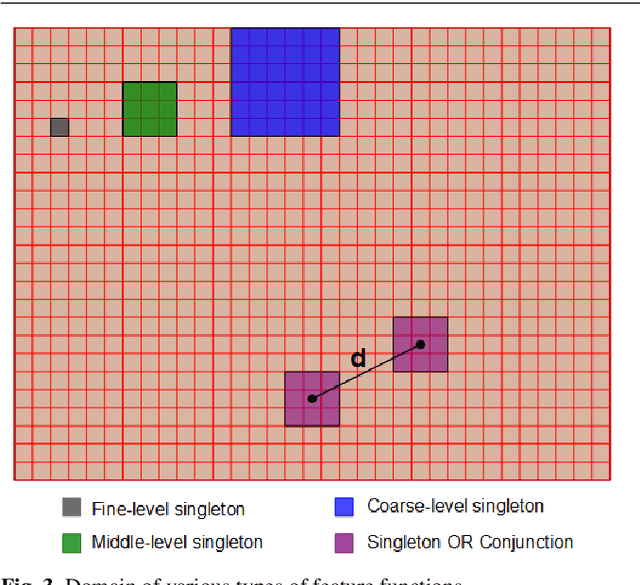
Despite enormous progress in object detection and classification, the problem of incorporating expected contextual relationships among object instances into modern recognition systems remains a key challenge. In this work we propose Information Pursuit, a Bayesian framework for scene parsing that combines prior models for the geometry of the scene and the spatial arrangement of objects instances with a data model for the output of high-level image classifiers trained to answer specific questions about the scene. In the proposed framework, the scene interpretation is progressively refined as evidence accumulates from the answers to a sequence of questions. At each step, we choose the question to maximize the mutual information between the new answer and the full interpretation given the current evidence obtained from previous inquiries. We also propose a method for learning the parameters of the model from synthesized, annotated scenes obtained by top-down sampling from an easy-to-learn generative scene model. Finally, we introduce a database of annotated indoor scenes of dining room tables, which we use to evaluate the proposed approach.

The Euler-Poincare theory of Metamorphosis

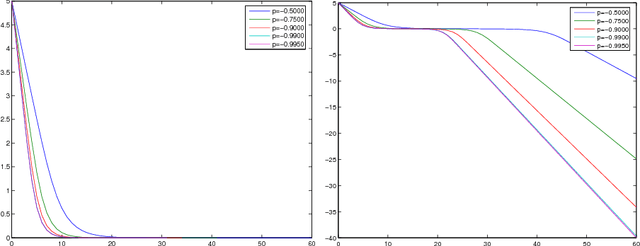
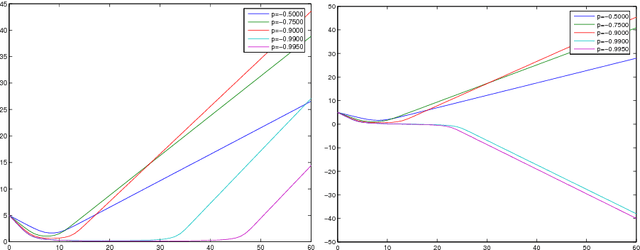
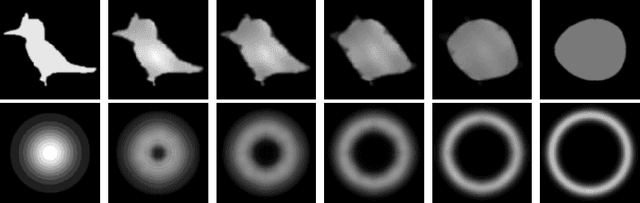
In the pattern matching approach to imaging science, the process of ``metamorphosis'' is template matching with dynamical templates. Here, we recast the metamorphosis equations of into the Euler-Poincare variational framework of and show that the metamorphosis equations contain the equations for a perfect complex fluid \cite{Ho2002}. This result connects the ideas underlying the process of metamorphosis in image matching to the physical concept of order parameter in the theory of complex fluids. After developing the general theory, we reinterpret various examples, including point set, image and density metamorphosis. We finally discuss the issue of matching measures with metamorphosis, for which we provide existence theorems for the initial and boundary value problems.