A continuous Structural Intervention Distance to compare Causal Graphs
Paper and Code
Jul 31, 2023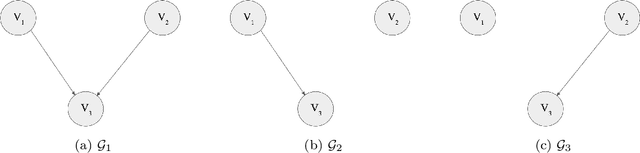
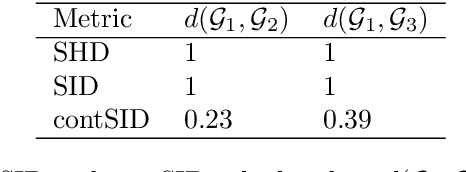
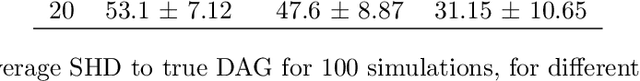
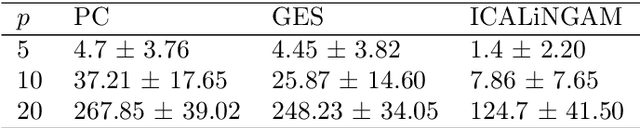
Understanding and adequately assessing the difference between a true and a learnt causal graphs is crucial for causal inference under interventions. As an extension to the graph-based structural Hamming distance and structural intervention distance, we propose a novel continuous-measured metric that considers the underlying data in addition to the graph structure for its calculation of the difference between a true and a learnt causal graph. The distance is based on embedding intervention distributions over each pair of nodes as conditional mean embeddings into reproducing kernel Hilbert spaces and estimating their difference by the maximum (conditional) mean discrepancy. We show theoretical results which we validate with numerical experiments on synthetic data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge