A fine-grained look at causal effects in causal spaces

The notion of causal effect is fundamental across many scientific disciplines. Traditionally, quantitative researchers have studied causal effects at the level of variables; for example, how a certain drug dose (W) causally affects a patient's blood pressure (Y). However, in many modern data domains, the raw variables-such as pixels in an image or tokens in a language model-do not have the semantic structure needed to formulate meaningful causal questions. In this paper, we offer a more fine-grained perspective by studying causal effects at the level of events, drawing inspiration from probability theory, where core notions such as independence are first given for events and sigma-algebras, before random variables enter the picture. Within the measure-theoretic framework of causal spaces, a recently introduced axiomatisation of causality, we first introduce several binary definitions that determine whether a causal effect is present, as well as proving some properties of them linking causal effect to (in)dependence under an intervention measure. Further, we provide quantifying measures that capture the strength and nature of causal effects on events, and show that we can recover the common measures of treatment effect as special cases.

Two Web Toolkits for Multimodal Piano Performance Dataset Acquisition and Fingering Annotation

Piano performance is a multimodal activity that intrinsically combines physical actions with the acoustic rendition. Despite growing research interest in analyzing the multimodal nature of piano performance, the laborious process of acquiring large-scale multimodal data remains a significant bottleneck, hindering further progress in this field. To overcome this barrier, we present an integrated web toolkit comprising two graphical user interfaces (GUIs): (i) PiaRec, which supports the synchronized acquisition of audio, video, MIDI, and performance metadata. (ii) ASDF, which enables the efficient annotation of performer fingering from the visual data. Collectively, this system can streamline the acquisition of multimodal piano performance datasets.

PianoVAM: A Multimodal Piano Performance Dataset

The multimodal nature of music performance has driven increasing interest in data beyond the audio domain within the music information retrieval (MIR) community. This paper introduces PianoVAM, a comprehensive piano performance dataset that includes videos, audio, MIDI, hand landmarks, fingering labels, and rich metadata. The dataset was recorded using a Disklavier piano, capturing audio and MIDI from amateur pianists during their daily practice sessions, alongside synchronized top-view videos in realistic and varied performance conditions. Hand landmarks and fingering labels were extracted using a pretrained hand pose estimation model and a semi-automated fingering annotation algorithm. We discuss the challenges encountered during data collection and the alignment process across different modalities. Additionally, we describe our fingering annotation method based on hand landmarks extracted from videos. Finally, we present benchmarking results for both audio-only and audio-visual piano transcription using the PianoVAM dataset and discuss additional potential applications.

On the sample complexity of semi-supervised multi-objective learning

In multi-objective learning (MOL), several possibly competing prediction tasks must be solved jointly by a single model. Achieving good trade-offs may require a model class $\mathcal{G}$ with larger capacity than what is necessary for solving the individual tasks. This, in turn, increases the statistical cost, as reflected in known MOL bounds that depend on the complexity of $\mathcal{G}$. We show that this cost is unavoidable for some losses, even in an idealized semi-supervised setting, where the learner has access to the Bayes-optimal solutions for the individual tasks as well as the marginal distributions over the covariates. On the other hand, for objectives defined with Bregman losses, we prove that the complexity of $\mathcal{G}$ may come into play only in terms of unlabeled data. Concretely, we establish sample complexity upper bounds, showing precisely when and how unlabeled data can significantly alleviate the need for labeled data. These rates are achieved by a simple, semi-supervised algorithm via pseudo-labeling.

A Classical View on Benign Overfitting: The Role of Sample Size

Benign overfitting is a phenomenon in machine learning where a model perfectly fits (interpolates) the training data, including noisy examples, yet still generalizes well to unseen data. Understanding this phenomenon has attracted considerable attention in recent years. In this work, we introduce a conceptual shift, by focusing on almost benign overfitting, where models simultaneously achieve both arbitrarily small training and test errors. This behavior is characteristic of neural networks, which often achieve low (but non-zero) training error while still generalizing well. We hypothesize that this almost benign overfitting can emerge even in classical regimes, by analyzing how the interaction between sample size and model complexity enables larger models to achieve both good training fit but still approach Bayes-optimal generalization. We substantiate this hypothesis with theoretical evidence from two case studies: (i) kernel ridge regression, and (ii) least-squares regression using a two-layer fully connected ReLU neural network trained via gradient flow. In both cases, we overcome the strong assumptions often required in prior work on benign overfitting. Our results on neural networks also provide the first generalization result in this setting that does not rely on any assumptions about the underlying regression function or noise, beyond boundedness. Our analysis introduces a novel proof technique based on decomposing the excess risk into estimation and approximation errors, interpreting gradient flow as an implicit regularizer, that helps avoid uniform convergence traps. This analysis idea could be of independent interest.

Benign Overfitting for Regression with Trained Two-Layer ReLU Networks

We study the least-square regression problem with a two-layer fully-connected neural network, with ReLU activation function, trained by gradient flow. Our first result is a generalization result, that requires no assumptions on the underlying regression function or the noise other than that they are bounded. We operate in the neural tangent kernel regime, and our generalization result is developed via a decomposition of the excess risk into estimation and approximation errors, viewing gradient flow as an implicit regularizer. This decomposition in the context of neural networks is a novel perspective of gradient descent, and helps us avoid uniform convergence traps. In this work, we also establish that under the same setting, the trained network overfits to the data. Together, these results, establishes the first result on benign overfitting for finite-width ReLU networks for arbitrary regression functions.

Particle swarm optimization with Applications to Maximum Likelihood Estimation and Penalized Negative Binomial Regression

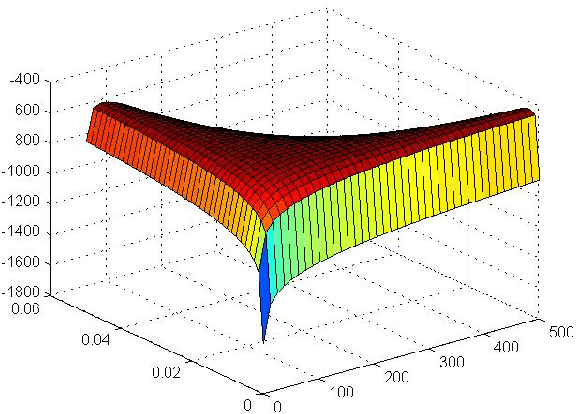
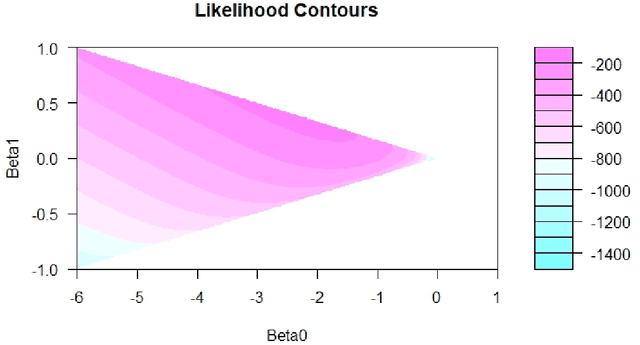
General purpose optimization routines such as nlminb, optim (R) or nlmixed (SAS) are frequently used to estimate model parameters in nonstandard distributions. This paper presents Particle Swarm Optimization (PSO), as an alternative to many of the current algorithms used in statistics. We find that PSO can not only reproduce the same results as the above routines, it can also produce results that are more optimal or when others cannot converge. In the latter case, it can also identify the source of the problem or problems. We highlight advantages of using PSO using four examples, where: (1) some parameters in a generalized distribution are unidentified using PSO when it is not apparent or computationally manifested using routines in R or SAS; (2) PSO can produce estimation results for the log-binomial regressions when current routines may not; (3) PSO provides flexibility in the link function for binomial regression with LASSO penalty, which is unsupported by standard packages like GLM and GENMOD in Stata and SAS, respectively, and (4) PSO provides superior MLE estimates for an EE-IW distribution compared with those from the traditional statistical methods that rely on moments.

A continuous Structural Intervention Distance to compare Causal Graphs

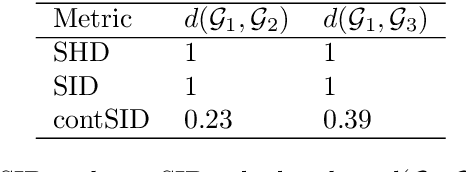
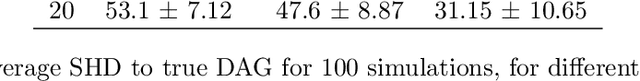
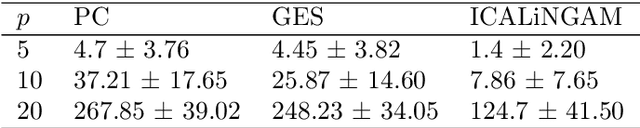
Understanding and adequately assessing the difference between a true and a learnt causal graphs is crucial for causal inference under interventions. As an extension to the graph-based structural Hamming distance and structural intervention distance, we propose a novel continuous-measured metric that considers the underlying data in addition to the graph structure for its calculation of the difference between a true and a learnt causal graph. The distance is based on embedding intervention distributions over each pair of nodes as conditional mean embeddings into reproducing kernel Hilbert spaces and estimating their difference by the maximum (conditional) mean discrepancy. We show theoretical results which we validate with numerical experiments on synthetic data.

Conditional Distributional Treatment Effect with Kernel Conditional Mean Embeddings and U-Statistic Regression

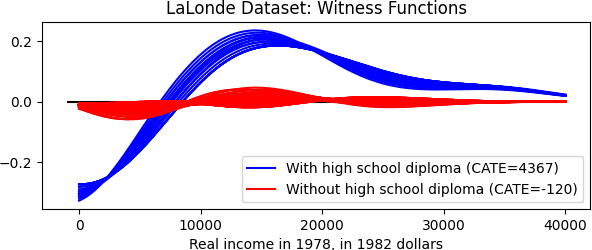
We propose to analyse the conditional distributional treatment effect (CoDiTE), which, in contrast to the more common conditional average treatment effect (CATE), is designed to encode a treatment's distributional aspects beyond the mean. We first introduce a formal definition of the CoDiTE associated with a distance function between probability measures. Then we discuss the CoDiTE associated with the maximum mean discrepancy via kernel conditional mean embeddings, which, coupled with a hypothesis test, tells us whether there is any conditional distributional effect of the treatment. Finally, we investigate what kind of conditional distributional effect the treatment has, both in an exploratory manner via the conditional witness function, and in a quantitative manner via U-statistic regression, generalising the CATE to higher-order moments. Experiments on synthetic, semi-synthetic and real datasets demonstrate the merits of our approach.

A Measure-Theoretic Approach to Kernel Conditional Mean Embeddings

We present a new operator-free, measure-theoretic definition of the conditional mean embedding as a random variable taking values in a reproducing kernel Hilbert space. While the kernel mean embedding of marginal distributions has been defined rigorously, the existing operator-based approach of the conditional version lacks a rigorous definition, and depends on strong assumptions that hinder its analysis. Our definition does not impose any of the assumptions that the operator-based counterpart requires. We derive a natural regression interpretation to obtain empirical estimates, and provide a thorough analysis of its properties, including universal consistency. As natural by-products, we obtain the conditional analogues of the Maximum Mean Discrepancy and Hilbert-Schmidt Independence Criterion, and demonstrate their behaviour via simulations.