A review of feature selection strategies utilizing graph data structures and knowledge graphs

Feature selection in Knowledge Graphs (KGs) are increasingly utilized in diverse domains, including biomedical research, Natural Language Processing (NLP), and personalized recommendation systems. This paper delves into the methodologies for feature selection within KGs, emphasizing their roles in enhancing machine learning (ML) model efficacy, hypothesis generation, and interpretability. Through this comprehensive review, we aim to catalyze further innovation in feature selection for KGs, paving the way for more insightful, efficient, and interpretable analytical models across various domains. Our exploration reveals the critical importance of scalability, accuracy, and interpretability in feature selection techniques, advocating for the integration of domain knowledge to refine the selection process. We highlight the burgeoning potential of multi-objective optimization and interdisciplinary collaboration in advancing KG feature selection, underscoring the transformative impact of such methodologies on precision medicine, among other fields. The paper concludes by charting future directions, including the development of scalable, dynamic feature selection algorithms and the integration of explainable AI principles to foster transparency and trust in KG-driven models.

A Metric-based Principal Curve Approach for Learning One-dimensional Manifold

Principal curve is a well-known statistical method oriented in manifold learning using concepts from differential geometry. In this paper, we propose a novel metric-based principal curve (MPC) method that learns one-dimensional manifold of spatial data. Synthetic datasets Real applications using MNIST dataset show that our method can learn the one-dimensional manifold well in terms of the shape.

Particle swarm optimization with Applications to Maximum Likelihood Estimation and Penalized Negative Binomial Regression

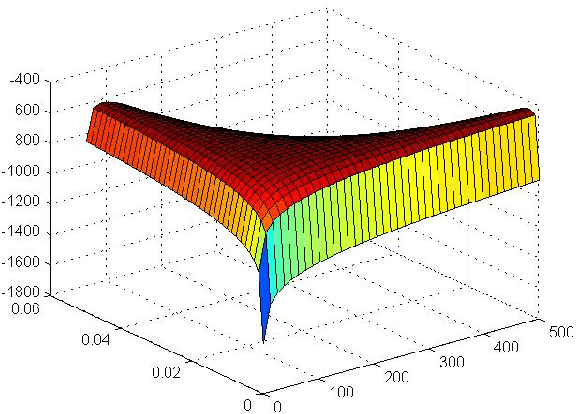
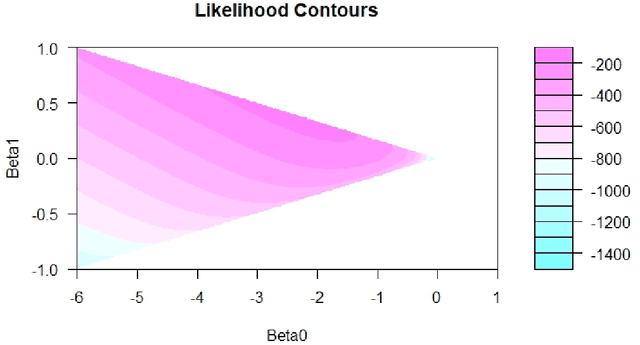
General purpose optimization routines such as nlminb, optim (R) or nlmixed (SAS) are frequently used to estimate model parameters in nonstandard distributions. This paper presents Particle Swarm Optimization (PSO), as an alternative to many of the current algorithms used in statistics. We find that PSO can not only reproduce the same results as the above routines, it can also produce results that are more optimal or when others cannot converge. In the latter case, it can also identify the source of the problem or problems. We highlight advantages of using PSO using four examples, where: (1) some parameters in a generalized distribution are unidentified using PSO when it is not apparent or computationally manifested using routines in R or SAS; (2) PSO can produce estimation results for the log-binomial regressions when current routines may not; (3) PSO provides flexibility in the link function for binomial regression with LASSO penalty, which is unsupported by standard packages like GLM and GENMOD in Stata and SAS, respectively, and (4) PSO provides superior MLE estimates for an EE-IW distribution compared with those from the traditional statistical methods that rely on moments.