A Semiparametric Bayesian Method for Instrumental Variable Analysis with Partly Interval-Censored Time-to-Event Outcome

This paper develops a semiparametric Bayesian instrumental variable analysis method for estimating the causal effect of an endogenous variable when dealing with unobserved confounders and measurement errors with partly interval-censored time-to-event data, where event times are observed exactly for some subjects but left-censored, right-censored, or interval-censored for others. Our method is based on a two-stage Dirichlet process mixture instrumental variable (DPMIV) model which simultaneously models the first-stage random error term for the exposure variable and the second-stage random error term for the time-to-event outcome using a bivariate Gaussian mixture of the Dirichlet process (DPM) model. The DPM model can be broadly understood as a mixture model with an unspecified number of Gaussian components, which relaxes the normal error assumptions and allows the number of mixture components to be determined by the data. We develop an MCMC algorithm for the DPMIV model tailored for partly interval-censored data and conduct extensive simulations to assess the performance of our DPMIV method in comparison with some competing methods. Our simulations revealed that our proposed method is robust under different error distributions and can have superior performance over its parametric counterpart under various scenarios. We further demonstrate the effectiveness of our approach on an UK Biobank data to investigate the causal effect of systolic blood pressure on time-to-development of cardiovascular disease from the onset of diabetes mellitus.

A Metric-based Principal Curve Approach for Learning One-dimensional Manifold

Principal curve is a well-known statistical method oriented in manifold learning using concepts from differential geometry. In this paper, we propose a novel metric-based principal curve (MPC) method that learns one-dimensional manifold of spatial data. Synthetic datasets Real applications using MNIST dataset show that our method can learn the one-dimensional manifold well in terms of the shape.

Metaheuristic Algorithms in Artificial Intelligence with Applications to Bioinformatics, Biostatistics, Ecology and, the Manufacturing Industries

Nature-inspired metaheuristic algorithms are important components of artificial intelligence, and are increasingly used across disciplines to tackle various types of challenging optimization problems. We apply a newly proposed nature-inspired metaheuristic algorithm called competitive swarm optimizer with mutated agents (CSO-MA) and demonstrate its flexibility and out-performance relative to its competitors in a variety of optimization problems in the statistical sciences. In particular, we show the algorithm is efficient and can incorporate various cost structures or multiple user-specified nonlinear constraints. Our applications include (i) finding maximum likelihood estimates of parameters in a single cell generalized trend model to study pseudotime in bioinformatics, (ii) estimating parameters in a commonly used Rasch model in education research, (iii) finding M-estimates for a Cox regression in a Markov renewal model and (iv) matrix completion to impute missing values in a two compartment model. In addition we discuss applications to (v) select variables optimally in an ecology problem and (vi) design a car refueling experiment for the auto industry using a logistic model with multiple interacting factors.

Dual Path Structural Contrastive Embeddings for Learning Novel Objects

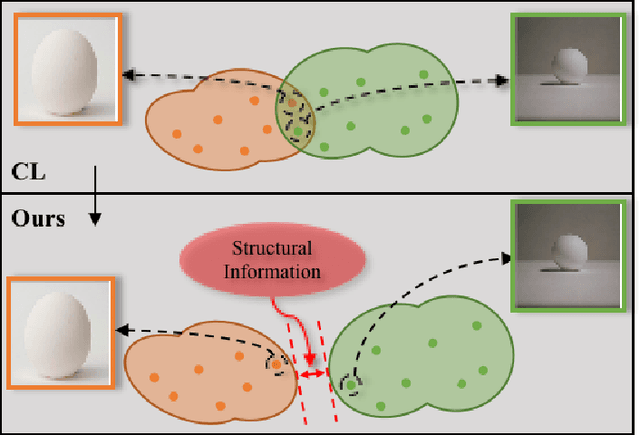
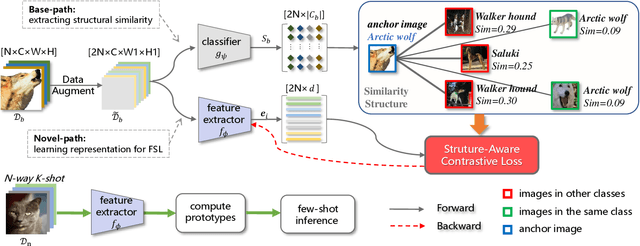
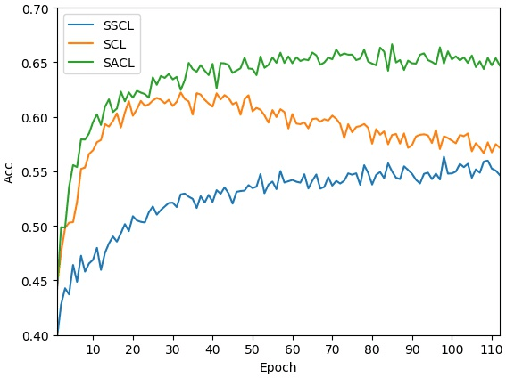
Learning novel classes from a very few labeled samples has attracted increasing attention in machine learning areas. Recent research on either meta-learning based or transfer-learning based paradigm demonstrates that gaining information on a good feature space can be an effective solution to achieve favorable performance on few-shot tasks. In this paper, we propose a simple but effective paradigm that decouples the tasks of learning feature representations and classifiers and only learns the feature embedding architecture from base classes via the typical transfer-learning training strategy. To maintain both the generalization ability across base and novel classes and discrimination ability within each class, we propose a dual path feature learning scheme that effectively combines structural similarity with contrastive feature construction. In this way, both inner-class alignment and inter-class uniformity can be well balanced, and result in improved performance. Experiments on three popular benchmarks show that when incorporated with a simple prototype based classifier, our method can still achieve promising results for both standard and generalized few-shot problems in either an inductive or transductive inference setting.