Distinct Computations Emerge From Compositional Curricula in In-Context Learning

In-context learning (ICL) research often considers learning a function in-context through a uniform sample of input-output pairs. Here, we investigate how presenting a compositional subtask curriculum in context may alter the computations a transformer learns. We design a compositional algorithmic task based on the modular exponential-a double exponential task composed of two single exponential subtasks and train transformer models to learn the task in-context. We compare (a) models trained using an in-context curriculum consisting of single exponential subtasks and, (b) models trained directly on the double exponential task without such a curriculum. We show that models trained with a subtask curriculum can perform zero-shot inference on unseen compositional tasks and are more robust given the same context length. We study how the task and subtasks are represented across the two training regimes. We find that the models employ diverse strategies modulated by the specific curriculum design.

Make Haste Slowly: A Theory of Emergent Structured Mixed Selectivity in Feature Learning ReLU Networks

In spite of finite dimension ReLU neural networks being a consistent factor behind recent deep learning successes, a theory of feature learning in these models remains elusive. Currently, insightful theories still rely on assumptions including the linearity of the network computations, unstructured input data and architectural constraints such as infinite width or a single hidden layer. To begin to address this gap we establish an equivalence between ReLU networks and Gated Deep Linear Networks, and use their greater tractability to derive dynamics of learning. We then consider multiple variants of a core task reminiscent of multi-task learning or contextual control which requires both feature learning and nonlinearity. We make explicit that, for these tasks, the ReLU networks possess an inductive bias towards latent representations which are not strictly modular or disentangled but are still highly structured and reusable between contexts. This effect is amplified with the addition of more contexts and hidden layers. Thus, we take a step towards a theory of feature learning in finite ReLU networks and shed light on how structured mixed-selective latent representations can emerge due to a bias for node-reuse and learning speed.

Strategy Coopetition Explains the Emergence and Transience of In-Context Learning

In-context learning (ICL) is a powerful ability that emerges in transformer models, enabling them to learn from context without weight updates. Recent work has established emergent ICL as a transient phenomenon that can sometimes disappear after long training times. In this work, we sought a mechanistic understanding of these transient dynamics. Firstly, we find that, after the disappearance of ICL, the asymptotic strategy is a remarkable hybrid between in-weights and in-context learning, which we term "context-constrained in-weights learning" (CIWL). CIWL is in competition with ICL, and eventually replaces it as the dominant strategy of the model (thus leading to ICL transience). However, we also find that the two competing strategies actually share sub-circuits, which gives rise to cooperative dynamics as well. For example, in our setup, ICL is unable to emerge quickly on its own, and can only be enabled through the simultaneous slow development of asymptotic CIWL. CIWL thus both cooperates and competes with ICL, a phenomenon we term "strategy coopetition." We propose a minimal mathematical model that reproduces these key dynamics and interactions. Informed by this model, we were able to identify a setup where ICL is truly emergent and persistent.

Nonlinear dynamics of localization in neural receptive fields

Localized receptive fields -- neurons that are selective for certain contiguous spatiotemporal features of their input -- populate early sensory regions of the mammalian brain. Unsupervised learning algorithms that optimize explicit sparsity or independence criteria replicate features of these localized receptive fields, but fail to explain directly how localization arises through learning without efficient coding, as occurs in early layers of deep neural networks and might occur in early sensory regions of biological systems. We consider an alternative model in which localized receptive fields emerge without explicit top-down efficiency constraints -- a feedforward neural network trained on a data model inspired by the structure of natural images. Previous work identified the importance of non-Gaussian statistics to localization in this setting but left open questions about the mechanisms driving dynamical emergence. We address these questions by deriving the effective learning dynamics for a single nonlinear neuron, making precise how higher-order statistical properties of the input data drive emergent localization, and we demonstrate that the predictions of these effective dynamics extend to the many-neuron setting. Our analysis provides an alternative explanation for the ubiquity of localization as resulting from the nonlinear dynamics of learning in neural circuits.

Flexible task abstractions emerge in linear networks with fast and bounded units

Animals survive in dynamic environments changing at arbitrary timescales, but such data distribution shifts are a challenge to neural networks. To adapt to change, neural systems may change a large number of parameters, which is a slow process involving forgetting past information. In contrast, animals leverage distribution changes to segment their stream of experience into tasks and associate them with internal task abstracts. Animals can then respond flexibly by selecting the appropriate task abstraction. However, how such flexible task abstractions may arise in neural systems remains unknown. Here, we analyze a linear gated network where the weights and gates are jointly optimized via gradient descent, but with neuron-like constraints on the gates including a faster timescale, nonnegativity, and bounded activity. We observe that the weights self-organize into modules specialized for tasks or sub-tasks encountered, while the gates layer forms unique representations that switch the appropriate weight modules (task abstractions). We analytically reduce the learning dynamics to an effective eigenspace, revealing a virtuous cycle: fast adapting gates drive weight specialization by protecting previous knowledge, while weight specialization in turn increases the update rate of the gating layer. Task switching in the gating layer accelerates as a function of curriculum block size and task training, mirroring key findings in cognitive neuroscience. We show that the discovered task abstractions support generalization through both task and subtask composition, and we extend our findings to a non-linear network switching between two tasks. Overall, our work offers a theory of cognitive flexibility in animals as arising from joint gradient descent on synaptic and neural gating in a neural network architecture.

From Lazy to Rich: Exact Learning Dynamics in Deep Linear Networks

Biological and artificial neural networks develop internal representations that enable them to perform complex tasks. In artificial networks, the effectiveness of these models relies on their ability to build task specific representation, a process influenced by interactions among datasets, architectures, initialization strategies, and optimization algorithms. Prior studies highlight that different initializations can place networks in either a lazy regime, where representations remain static, or a rich/feature learning regime, where representations evolve dynamically. Here, we examine how initialization influences learning dynamics in deep linear neural networks, deriving exact solutions for lambda-balanced initializations-defined by the relative scale of weights across layers. These solutions capture the evolution of representations and the Neural Tangent Kernel across the spectrum from the rich to the lazy regimes. Our findings deepen the theoretical understanding of the impact of weight initialization on learning regimes, with implications for continual learning, reversal learning, and transfer learning, relevant to both neuroscience and practical applications.

What needs to go right for an induction head? A mechanistic study of in-context learning circuits and their formation

In-context learning is a powerful emergent ability in transformer models. Prior work in mechanistic interpretability has identified a circuit element that may be critical for in-context learning -- the induction head (IH), which performs a match-and-copy operation. During training of large transformers on natural language data, IHs emerge around the same time as a notable phase change in the loss. Despite the robust evidence for IHs and this interesting coincidence with the phase change, relatively little is known about the diversity and emergence dynamics of IHs. Why is there more than one IH, and how are they dependent on each other? Why do IHs appear all of a sudden, and what are the subcircuits that enable them to emerge? We answer these questions by studying IH emergence dynamics in a controlled setting by training on synthetic data. In doing so, we develop and share a novel optogenetics-inspired causal framework for modifying activations throughout training. Using this framework, we delineate the diverse and additive nature of IHs. By clamping subsets of activations throughout training, we then identify three underlying subcircuits that interact to drive IH formation, yielding the phase change. Furthermore, these subcircuits shed light on data-dependent properties of formation, such as phase change timing, already showing the promise of this more in-depth understanding of subcircuits that need to "go right" for an induction head.

When Representations Align: Universality in Representation Learning Dynamics

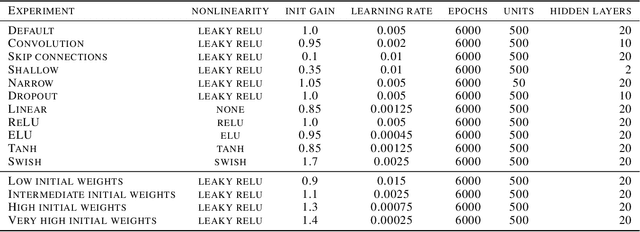
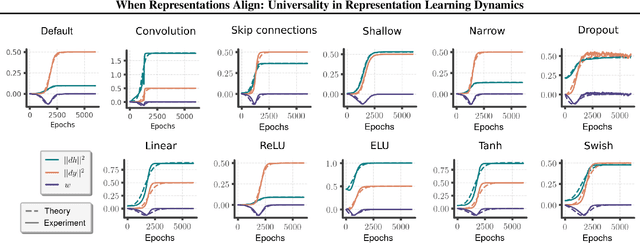
Deep neural networks come in many sizes and architectures. The choice of architecture, in conjunction with the dataset and learning algorithm, is commonly understood to affect the learned neural representations. Yet, recent results have shown that different architectures learn representations with striking qualitative similarities. Here we derive an effective theory of representation learning under the assumption that the encoding map from input to hidden representation and the decoding map from representation to output are arbitrary smooth functions. This theory schematizes representation learning dynamics in the regime of complex, large architectures, where hidden representations are not strongly constrained by the parametrization. We show through experiments that the effective theory describes aspects of representation learning dynamics across a range of deep networks with different activation functions and architectures, and exhibits phenomena similar to the "rich" and "lazy" regime. While many network behaviors depend quantitatively on architecture, our findings point to certain behaviors that are widely conserved once models are sufficiently flexible.

The Transient Nature of Emergent In-Context Learning in Transformers

Transformer neural networks can exhibit a surprising capacity for in-context learning (ICL) despite not being explicitly trained for it. Prior work has provided a deeper understanding of how ICL emerges in transformers, e.g. through the lens of mechanistic interpretability, Bayesian inference, or by examining the distributional properties of training data. However, in each of these cases, ICL is treated largely as a persistent phenomenon; namely, once ICL emerges, it is assumed to persist asymptotically. Here, we show that the emergence of ICL during transformer training is, in fact, often transient. We train transformers on synthetic data designed so that both ICL and in-weights learning (IWL) strategies can lead to correct predictions. We find that ICL first emerges, then disappears and gives way to IWL, all while the training loss decreases, indicating an asymptotic preference for IWL. The transient nature of ICL is observed in transformers across a range of model sizes and datasets, raising the question of how much to "overtrain" transformers when seeking compact, cheaper-to-run models. We find that L2 regularization may offer a path to more persistent ICL that removes the need for early stopping based on ICL-style validation tasks. Finally, we present initial evidence that ICL transience may be caused by competition between ICL and IWL circuits.

Meta-Learning Strategies through Value Maximization in Neural Networks

Biological and artificial learning agents face numerous choices about how to learn, ranging from hyperparameter selection to aspects of task distributions like curricula. Understanding how to make these meta-learning choices could offer normative accounts of cognitive control functions in biological learners and improve engineered systems. Yet optimal strategies remain challenging to compute in modern deep networks due to the complexity of optimizing through the entire learning process. Here we theoretically investigate optimal strategies in a tractable setting. We present a learning effort framework capable of efficiently optimizing control signals on a fully normative objective: discounted cumulative performance throughout learning. We obtain computational tractability by using average dynamical equations for gradient descent, available for simple neural network architectures. Our framework accommodates a range of meta-learning and automatic curriculum learning methods in a unified normative setting. We apply this framework to investigate the effect of approximations in common meta-learning algorithms; infer aspects of optimal curricula; and compute optimal neuronal resource allocation in a continual learning setting. Across settings, we find that control effort is most beneficial when applied to easier aspects of a task early in learning; followed by sustained effort on harder aspects. Overall, the learning effort framework provides a tractable theoretical test bed to study normative benefits of interventions in a variety of learning systems, as well as a formal account of optimal cognitive control strategies over learning trajectories posited by established theories in cognitive neuroscience.