Flexible task abstractions emerge in linear networks with fast and bounded units

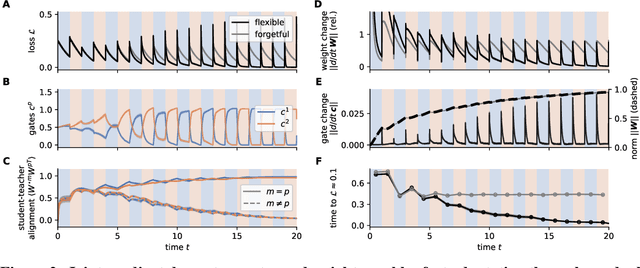
Animals survive in dynamic environments changing at arbitrary timescales, but such data distribution shifts are a challenge to neural networks. To adapt to change, neural systems may change a large number of parameters, which is a slow process involving forgetting past information. In contrast, animals leverage distribution changes to segment their stream of experience into tasks and associate them with internal task abstracts. Animals can then respond flexibly by selecting the appropriate task abstraction. However, how such flexible task abstractions may arise in neural systems remains unknown. Here, we analyze a linear gated network where the weights and gates are jointly optimized via gradient descent, but with neuron-like constraints on the gates including a faster timescale, nonnegativity, and bounded activity. We observe that the weights self-organize into modules specialized for tasks or sub-tasks encountered, while the gates layer forms unique representations that switch the appropriate weight modules (task abstractions). We analytically reduce the learning dynamics to an effective eigenspace, revealing a virtuous cycle: fast adapting gates drive weight specialization by protecting previous knowledge, while weight specialization in turn increases the update rate of the gating layer. Task switching in the gating layer accelerates as a function of curriculum block size and task training, mirroring key findings in cognitive neuroscience. We show that the discovered task abstractions support generalization through both task and subtask composition, and we extend our findings to a non-linear network switching between two tasks. Overall, our work offers a theory of cognitive flexibility in animals as arising from joint gradient descent on synaptic and neural gating in a neural network architecture.

Early learning of the optimal constant solution in neural networks and humans

Deep neural networks learn increasingly complex functions over the course of training. Here, we show both empirically and theoretically that learning of the target function is preceded by an early phase in which networks learn the optimal constant solution (OCS) - that is, initial model responses mirror the distribution of target labels, while entirely ignoring information provided in the input. Using a hierarchical category learning task, we derive exact solutions for learning dynamics in deep linear networks trained with bias terms. Even when initialized to zero, this simple architectural feature induces substantial changes in early dynamics. We identify hallmarks of this early OCS phase and illustrate how these signatures are observed in deep linear networks and larger, more complex (and nonlinear) convolutional neural networks solving a hierarchical learning task based on MNIST and CIFAR10. We explain these observations by proving that deep linear networks necessarily learn the OCS during early learning. To further probe the generality of our results, we train human learners over the course of three days on the category learning task. We then identify qualitative signatures of this early OCS phase in terms of the dynamics of true negative (correct-rejection) rates. Surprisingly, we find the same early reliance on the OCS in the behaviour of human learners. Finally, we show that learning of the OCS can emerge even in the absence of bias terms and is equivalently driven by generic correlations in the input data. Overall, our work suggests the OCS as a universal learning principle in supervised, error-corrective learning, and the mechanistic reasons for its prevalence.