When Representations Align: Universality in Representation Learning Dynamics
Paper and Code
Feb 14, 2024
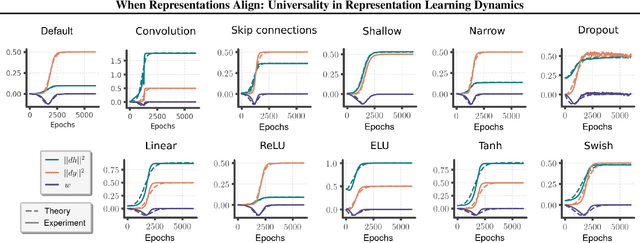

Deep neural networks come in many sizes and architectures. The choice of architecture, in conjunction with the dataset and learning algorithm, is commonly understood to affect the learned neural representations. Yet, recent results have shown that different architectures learn representations with striking qualitative similarities. Here we derive an effective theory of representation learning under the assumption that the encoding map from input to hidden representation and the decoding map from representation to output are arbitrary smooth functions. This theory schematizes representation learning dynamics in the regime of complex, large architectures, where hidden representations are not strongly constrained by the parametrization. We show through experiments that the effective theory describes aspects of representation learning dynamics across a range of deep networks with different activation functions and architectures, and exhibits phenomena similar to the "rich" and "lazy" regime. While many network behaviors depend quantitatively on architecture, our findings point to certain behaviors that are widely conserved once models are sufficiently flexible.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge