From Lazy to Rich: Exact Learning Dynamics in Deep Linear Networks

Biological and artificial neural networks develop internal representations that enable them to perform complex tasks. In artificial networks, the effectiveness of these models relies on their ability to build task specific representation, a process influenced by interactions among datasets, architectures, initialization strategies, and optimization algorithms. Prior studies highlight that different initializations can place networks in either a lazy regime, where representations remain static, or a rich/feature learning regime, where representations evolve dynamically. Here, we examine how initialization influences learning dynamics in deep linear neural networks, deriving exact solutions for lambda-balanced initializations-defined by the relative scale of weights across layers. These solutions capture the evolution of representations and the Neural Tangent Kernel across the spectrum from the rich to the lazy regimes. Our findings deepen the theoretical understanding of the impact of weight initialization on learning regimes, with implications for continual learning, reversal learning, and transfer learning, relevant to both neuroscience and practical applications.

Get rich quick: exact solutions reveal how unbalanced initializations promote rapid feature learning

While the impressive performance of modern neural networks is often attributed to their capacity to efficiently extract task-relevant features from data, the mechanisms underlying this rich feature learning regime remain elusive, with much of our theoretical understanding stemming from the opposing lazy regime. In this work, we derive exact solutions to a minimal model that transitions between lazy and rich learning, precisely elucidating how unbalanced layer-specific initialization variances and learning rates determine the degree of feature learning. Our analysis reveals that they conspire to influence the learning regime through a set of conserved quantities that constrain and modify the geometry of learning trajectories in parameter and function space. We extend our analysis to more complex linear models with multiple neurons, outputs, and layers and to shallow nonlinear networks with piecewise linear activation functions. In linear networks, rapid feature learning only occurs with balanced initializations, where all layers learn at similar speeds. While in nonlinear networks, unbalanced initializations that promote faster learning in earlier layers can accelerate rich learning. Through a series of experiments, we provide evidence that this unbalanced rich regime drives feature learning in deep finite-width networks, promotes interpretability of early layers in CNNs, reduces the sample complexity of learning hierarchical data, and decreases the time to grokking in modular arithmetic. Our theory motivates further exploration of unbalanced initializations to enhance efficient feature learning.

Stochastic Collapse: How Gradient Noise Attracts SGD Dynamics Towards Simpler Subnetworks

In this work, we reveal a strong implicit bias of stochastic gradient descent (SGD) that drives overly expressive networks to much simpler subnetworks, thereby dramatically reducing the number of independent parameters, and improving generalization. To reveal this bias, we identify invariant sets, or subsets of parameter space that remain unmodified by SGD. We focus on two classes of invariant sets that correspond to simpler subnetworks and commonly appear in modern architectures. Our analysis uncovers that SGD exhibits a property of stochastic attractivity towards these simpler invariant sets. We establish a sufficient condition for stochastic attractivity based on a competition between the loss landscape's curvature around the invariant set and the noise introduced by stochastic gradients. Remarkably, we find that an increased level of noise strengthens attractivity, leading to the emergence of attractive invariant sets associated with saddle-points or local maxima of the train loss. We observe empirically the existence of attractive invariant sets in trained deep neural networks, implying that SGD dynamics often collapses to simple subnetworks with either vanishing or redundant neurons. We further demonstrate how this simplifying process of stochastic collapse benefits generalization in a linear teacher-student framework. Finally, through this analysis, we mechanistically explain why early training with large learning rates for extended periods benefits subsequent generalization.

The Asymmetric Maximum Margin Bias of Quasi-Homogeneous Neural Networks

In this work, we explore the maximum-margin bias of quasi-homogeneous neural networks trained with gradient flow on an exponential loss and past a point of separability. We introduce the class of quasi-homogeneous models, which is expressive enough to describe nearly all neural networks with homogeneous activations, even those with biases, residual connections, and normalization layers, while structured enough to enable geometric analysis of its gradient dynamics. Using this analysis, we generalize the existing results of maximum-margin bias for homogeneous networks to this richer class of models. We find that gradient flow implicitly favors a subset of the parameters, unlike in the case of a homogeneous model where all parameters are treated equally. We demonstrate through simple examples how this strong favoritism toward minimizing an asymmetric norm can degrade the robustness of quasi-homogeneous models. On the other hand, we conjecture that this norm-minimization discards, when possible, unnecessary higher-order parameters, reducing the model to a sparser parameterization. Lastly, by applying our theorem to sufficiently expressive neural networks with normalization layers, we reveal a universal mechanism behind the empirical phenomenon of Neural Collapse.

Rethinking the limiting dynamics of SGD: modified loss, phase space oscillations, and anomalous diffusion

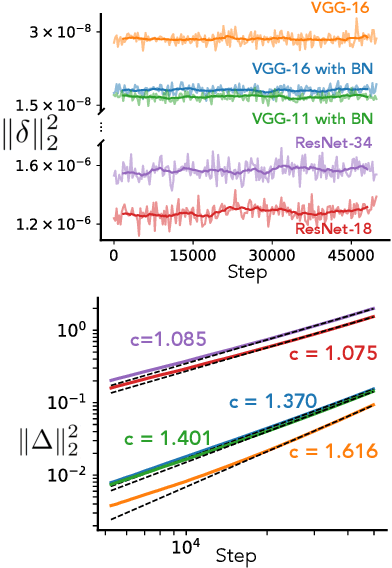
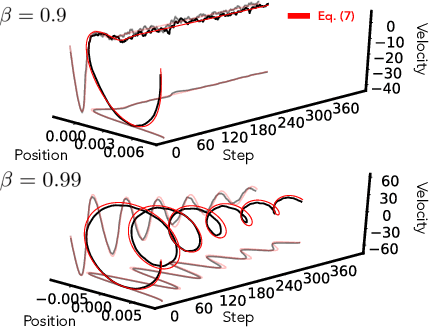
In this work we explore the limiting dynamics of deep neural networks trained with stochastic gradient descent (SGD). We find empirically that long after performance has converged, networks continue to move through parameter space by a process of anomalous diffusion in which distance travelled grows as a power law in the number of gradient updates with a nontrivial exponent. We reveal an intricate interaction between the hyperparameters of optimization, the structure in the gradient noise, and the Hessian matrix at the end of training that explains this anomalous diffusion. To build this understanding, we first derive a continuous-time model for SGD with finite learning rates and batch sizes as an underdamped Langevin equation. We study this equation in the setting of linear regression, where we can derive exact, analytic expressions for the phase space dynamics of the parameters and their instantaneous velocities from initialization to stationarity. Using the Fokker-Planck equation, we show that the key ingredient driving these dynamics is not the original training loss, but rather the combination of a modified loss, which implicitly regularizes the velocity, and probability currents, which cause oscillations in phase space. We identify qualitative and quantitative predictions of this theory in the dynamics of a ResNet-18 model trained on ImageNet. Through the lens of statistical physics, we uncover a mechanistic origin for the anomalous limiting dynamics of deep neural networks trained with SGD.

Noether's Learning Dynamics: The Role of Kinetic Symmetry Breaking in Deep Learning

In nature, symmetry governs regularities, while symmetry breaking brings texture. Here, we reveal a novel role of symmetry breaking behind efficiency and stability in learning, a critical issue in machine learning. Recent experiments suggest that the symmetry of the loss function is closely related to the learning performance. This raises a fundamental question. Is such symmetry beneficial, harmful, or irrelevant to the success of learning? Here, we demystify this question and pose symmetry breaking as a new design principle by considering the symmetry of the learning rule in addition to the loss function. We model the discrete learning dynamics using a continuous-time Lagrangian formulation, in which the learning rule corresponds to the kinetic energy and the loss function corresponds to the potential energy. We identify kinetic asymmetry unique to learning systems, where the kinetic energy often does not have the same symmetry as the potential (loss) function reflecting the non-physical symmetries of the loss function and the non-Euclidean metric used in learning rules. We generalize Noether's theorem known in physics to explicitly take into account this kinetic asymmetry and derive the resulting motion of the Noether charge. Finally, we apply our theory to modern deep networks with normalization layers and reveal a mechanism of implicit adaptive optimization induced by the kinetic symmetry breaking.

Neural Mechanics: Symmetry and Broken Conservation Laws in Deep Learning Dynamics

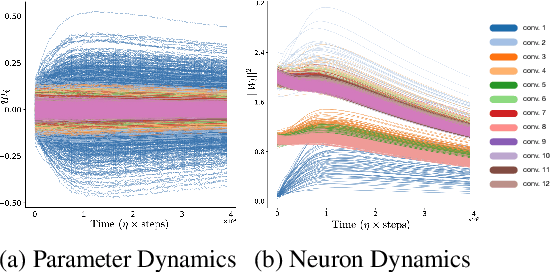
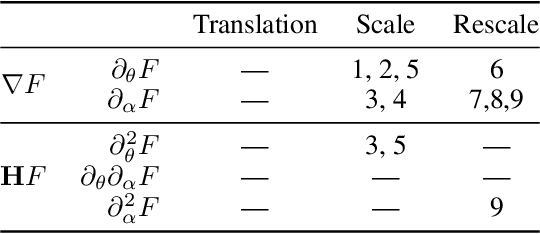
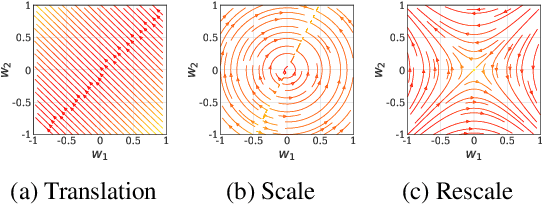
Predicting the dynamics of neural network parameters during training is one of the key challenges in building a theoretical foundation for deep learning. A central obstacle is that the motion of a network in high-dimensional parameter space undergoes discrete finite steps along complex stochastic gradients derived from real-world datasets. We circumvent this obstacle through a unifying theoretical framework based on intrinsic symmetries embedded in a network's architecture that are present for any dataset. We show that any such symmetry imposes stringent geometric constraints on gradients and Hessians, leading to an associated conservation law in the continuous-time limit of stochastic gradient descent (SGD), akin to Noether's theorem in physics. We further show that finite learning rates used in practice can actually break these symmetry induced conservation laws. We apply tools from finite difference methods to derive modified gradient flow, a differential equation that better approximates the numerical trajectory taken by SGD at finite learning rates. We combine modified gradient flow with our framework of symmetries to derive exact integral expressions for the dynamics of certain parameter combinations. We empirically validate our analytic predictions for learning dynamics on VGG-16 trained on Tiny ImageNet. Overall, by exploiting symmetry, our work demonstrates that we can analytically describe the learning dynamics of various parameter combinations at finite learning rates and batch sizes for state of the art architectures trained on any dataset.

Pruning neural networks without any data by iteratively conserving synaptic flow

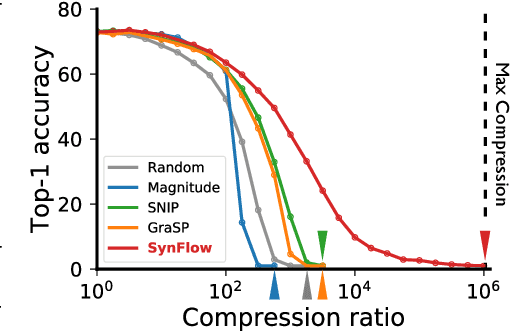
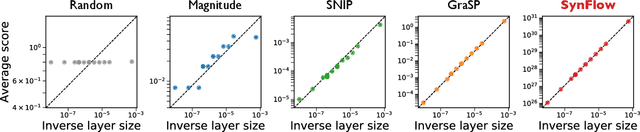
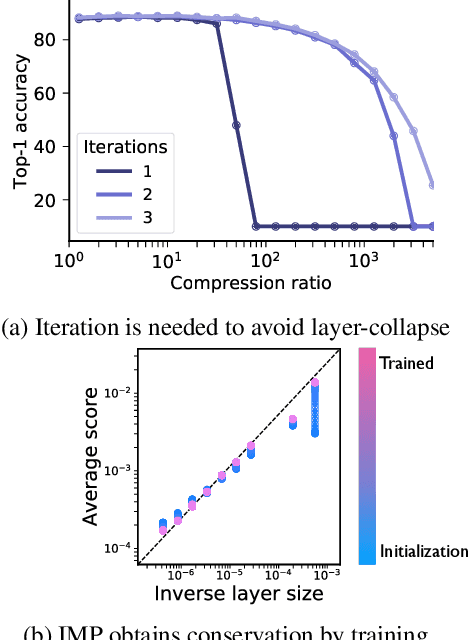
Pruning the parameters of deep neural networks has generated intense interest due to potential savings in time, memory and energy both during training and at test time. Recent works have identified, through an expensive sequence of training and pruning cycles, the existence of winning lottery tickets or sparse trainable subnetworks at initialization. This raises a foundational question: can we identify highly sparse trainable subnetworks at initialization, without ever training, or indeed without ever looking at the data? We provide an affirmative answer to this question through theory driven algorithm design. We first mathematically formulate and experimentally verify a conservation law that explains why existing gradient-based pruning algorithms at initialization suffer from layer-collapse, the premature pruning of an entire layer rendering a network untrainable. This theory also elucidates how layer-collapse can be entirely avoided, motivating a novel pruning algorithm Iterative Synaptic Flow Pruning (SynFlow). This algorithm can be interpreted as preserving the total flow of synaptic strengths through the network at initialization subject to a sparsity constraint. Notably, this algorithm makes no reference to the training data and consistently outperforms existing state-of-the-art pruning algorithms at initialization over a range of models (VGG and ResNet), datasets (CIFAR-10/100 and Tiny ImageNet), and sparsity constraints (up to 99.9 percent). Thus our data-agnostic pruning algorithm challenges the existing paradigm that data must be used to quantify which synapses are important.

Two Routes to Scalable Credit Assignment without Weight Symmetry

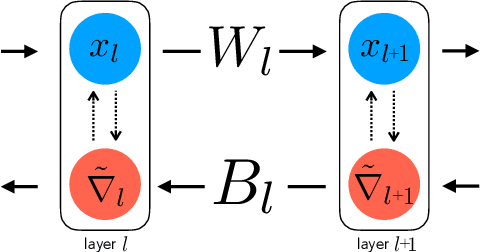
The neural plausibility of backpropagation has long been disputed, primarily for its use of non-local weight transport - the biologically dubious requirement that one neuron instantaneously measure the synaptic weights of another. Until recently, attempts to create local learning rules that avoid weight transport have typically failed in the large-scale learning scenarios where backpropagation shines, e.g. ImageNet categorization with deep convolutional networks. Here, we investigate a recently proposed local learning rule that yields competitive performance with backpropagation and find that it is highly sensitive to metaparameter choices, requiring laborious tuning that does not transfer across network architecture. Our analysis indicates the underlying mathematical reason for this instability, allowing us to identify a more robust local learning rule that better transfers without metaparameter tuning. Nonetheless, we find a performance and stability gap between this local rule and backpropagation that widens with increasing model depth. We then investigate several non-local learning rules that relax the need for instantaneous weight transport into a more biologically-plausible "weight estimation" process, showing that these rules match state-of-the-art performance on deep networks and operate effectively in the presence of noisy updates. Taken together, our results suggest two routes towards the discovery of neural implementations for credit assignment without weight symmetry: further improvement of local rules so that they perform consistently across architectures and the identification of biological implementations for non-local learning mechanisms.

Loss Landscapes of Regularized Linear Autoencoders

Autoencoders are a deep learning model for representation learning. When trained to minimize the Euclidean distance between the data and its reconstruction, linear autoencoders (LAEs) learn the subspace spanned by the top principal directions but cannot learn the principal directions themselves. In this paper, we prove that $L_2$-regularized LAEs learn the principal directions as the left singular vectors of the decoder, providing an extremely simple and scalable algorithm for rank-$k$ SVD. More generally, we consider LAEs with (i) no regularization, (ii) regularization of the composition of the encoder and decoder, and (iii) regularization of the encoder and decoder separately. We relate the minimum of (iii) to the MAP estimate of probabilistic PCA and show that for all critical points the encoder and decoder are transposes. Building on topological intuition, we smoothly parameterize the critical manifolds for all three losses via a novel unified framework and illustrate these results empirically. Overall, this work clarifies the relationship between autoencoders and Bayesian models and between regularization and orthogonality.