Rethinking the limiting dynamics of SGD: modified loss, phase space oscillations, and anomalous diffusion

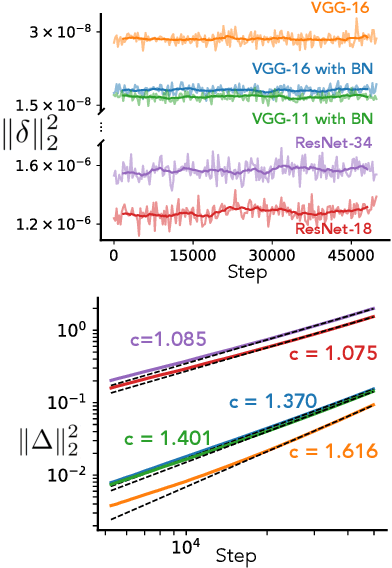
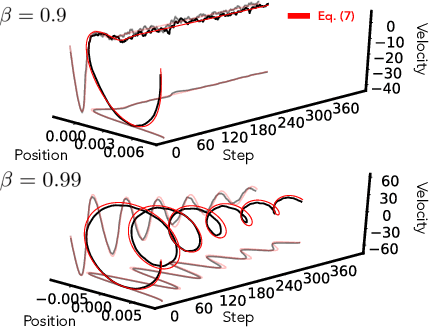
In this work we explore the limiting dynamics of deep neural networks trained with stochastic gradient descent (SGD). We find empirically that long after performance has converged, networks continue to move through parameter space by a process of anomalous diffusion in which distance travelled grows as a power law in the number of gradient updates with a nontrivial exponent. We reveal an intricate interaction between the hyperparameters of optimization, the structure in the gradient noise, and the Hessian matrix at the end of training that explains this anomalous diffusion. To build this understanding, we first derive a continuous-time model for SGD with finite learning rates and batch sizes as an underdamped Langevin equation. We study this equation in the setting of linear regression, where we can derive exact, analytic expressions for the phase space dynamics of the parameters and their instantaneous velocities from initialization to stationarity. Using the Fokker-Planck equation, we show that the key ingredient driving these dynamics is not the original training loss, but rather the combination of a modified loss, which implicitly regularizes the velocity, and probability currents, which cause oscillations in phase space. We identify qualitative and quantitative predictions of this theory in the dynamics of a ResNet-18 model trained on ImageNet. Through the lens of statistical physics, we uncover a mechanistic origin for the anomalous limiting dynamics of deep neural networks trained with SGD.

Validation and generalization of pixel-wise relevance in convolutional neural networks trained for face classification

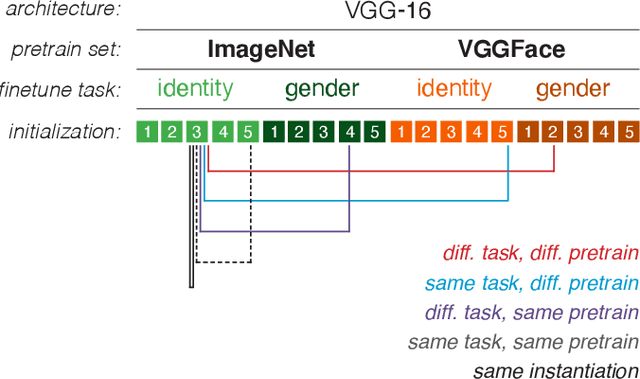
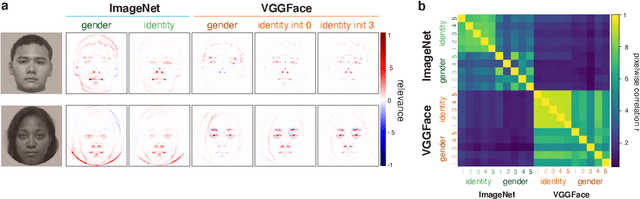
The increased use of convolutional neural networks for face recognition in science, governance, and broader society has created an acute need for methods that can show how these 'black box' decisions are made. To be interpretable and useful to humans, such a method should convey a model's learned classification strategy in a way that is robust to random initializations or spurious correlations in input data. To this end, we applied the decompositional pixel-wise attribution method of layer-wise relevance propagation (LRP) to resolve the decisions of several classes of VGG-16 models trained for face recognition. We then quantified how these relevance measures vary with and generalize across key model parameters, such as the pretraining dataset (ImageNet or VGGFace), the finetuning task (gender or identity classification), and random initializations of model weights. Using relevance-based image masking, we find that relevance maps for face classification prove generally stable across random initializations, and can generalize across finetuning tasks. However, there is markedly less generalization across pretraining datasets, indicating that ImageNet- and VGGFace-trained models sample face information differently even as they achieve comparably high classification performance. Fine-grained analyses of relevance maps across models revealed asymmetries in generalization that point to specific benefits of choice parameters, and suggest that it may be possible to find an underlying set of important face image pixels that drive decisions across convolutional neural networks and tasks. Finally, we evaluated model decision weighting against human measures of similarity, providing a novel framework for interpreting face recognition decisions across human and machine.