Rethinking the limiting dynamics of SGD: modified loss, phase space oscillations, and anomalous diffusion

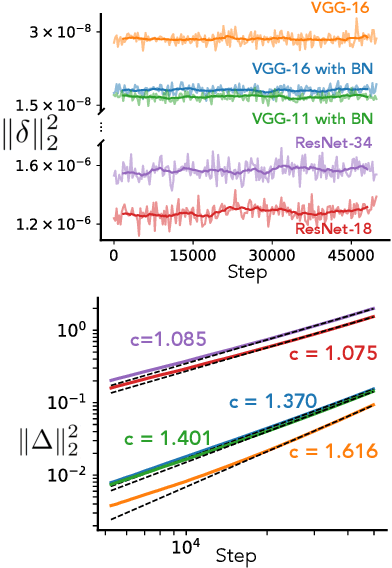
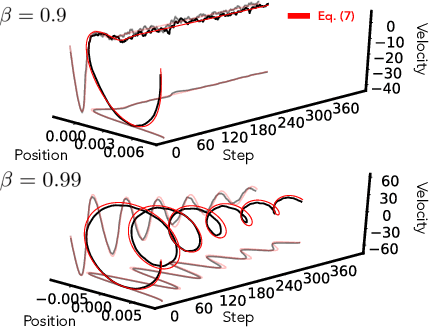
In this work we explore the limiting dynamics of deep neural networks trained with stochastic gradient descent (SGD). We find empirically that long after performance has converged, networks continue to move through parameter space by a process of anomalous diffusion in which distance travelled grows as a power law in the number of gradient updates with a nontrivial exponent. We reveal an intricate interaction between the hyperparameters of optimization, the structure in the gradient noise, and the Hessian matrix at the end of training that explains this anomalous diffusion. To build this understanding, we first derive a continuous-time model for SGD with finite learning rates and batch sizes as an underdamped Langevin equation. We study this equation in the setting of linear regression, where we can derive exact, analytic expressions for the phase space dynamics of the parameters and their instantaneous velocities from initialization to stationarity. Using the Fokker-Planck equation, we show that the key ingredient driving these dynamics is not the original training loss, but rather the combination of a modified loss, which implicitly regularizes the velocity, and probability currents, which cause oscillations in phase space. We identify qualitative and quantitative predictions of this theory in the dynamics of a ResNet-18 model trained on ImageNet. Through the lens of statistical physics, we uncover a mechanistic origin for the anomalous limiting dynamics of deep neural networks trained with SGD.

Neural Mechanics: Symmetry and Broken Conservation Laws in Deep Learning Dynamics

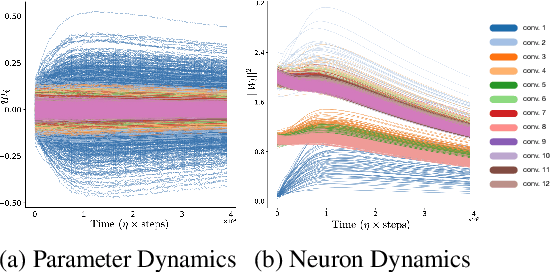
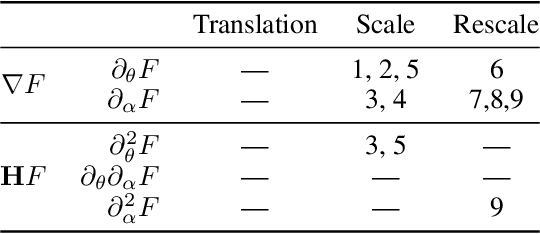
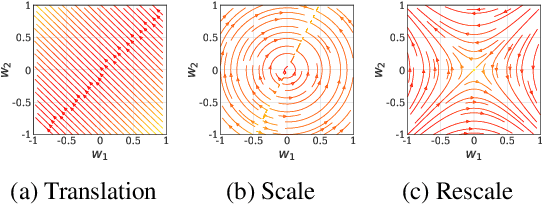
Predicting the dynamics of neural network parameters during training is one of the key challenges in building a theoretical foundation for deep learning. A central obstacle is that the motion of a network in high-dimensional parameter space undergoes discrete finite steps along complex stochastic gradients derived from real-world datasets. We circumvent this obstacle through a unifying theoretical framework based on intrinsic symmetries embedded in a network's architecture that are present for any dataset. We show that any such symmetry imposes stringent geometric constraints on gradients and Hessians, leading to an associated conservation law in the continuous-time limit of stochastic gradient descent (SGD), akin to Noether's theorem in physics. We further show that finite learning rates used in practice can actually break these symmetry induced conservation laws. We apply tools from finite difference methods to derive modified gradient flow, a differential equation that better approximates the numerical trajectory taken by SGD at finite learning rates. We combine modified gradient flow with our framework of symmetries to derive exact integral expressions for the dynamics of certain parameter combinations. We empirically validate our analytic predictions for learning dynamics on VGG-16 trained on Tiny ImageNet. Overall, by exploiting symmetry, our work demonstrates that we can analytically describe the learning dynamics of various parameter combinations at finite learning rates and batch sizes for state of the art architectures trained on any dataset.

Two Routes to Scalable Credit Assignment without Weight Symmetry

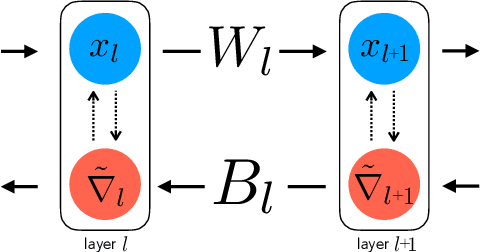
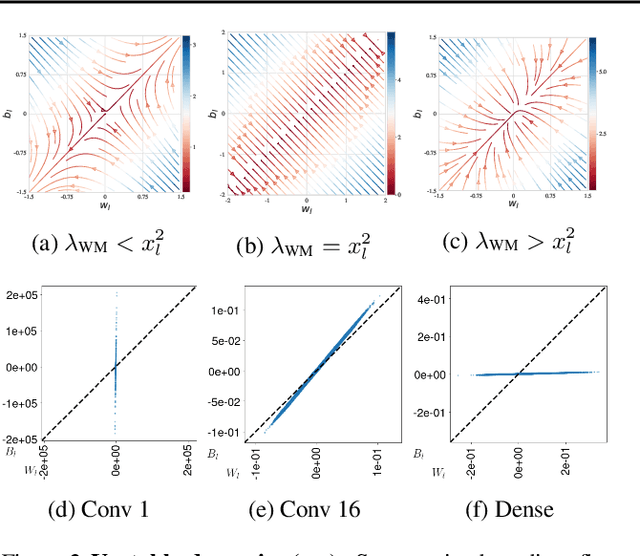
The neural plausibility of backpropagation has long been disputed, primarily for its use of non-local weight transport - the biologically dubious requirement that one neuron instantaneously measure the synaptic weights of another. Until recently, attempts to create local learning rules that avoid weight transport have typically failed in the large-scale learning scenarios where backpropagation shines, e.g. ImageNet categorization with deep convolutional networks. Here, we investigate a recently proposed local learning rule that yields competitive performance with backpropagation and find that it is highly sensitive to metaparameter choices, requiring laborious tuning that does not transfer across network architecture. Our analysis indicates the underlying mathematical reason for this instability, allowing us to identify a more robust local learning rule that better transfers without metaparameter tuning. Nonetheless, we find a performance and stability gap between this local rule and backpropagation that widens with increasing model depth. We then investigate several non-local learning rules that relax the need for instantaneous weight transport into a more biologically-plausible "weight estimation" process, showing that these rules match state-of-the-art performance on deep networks and operate effectively in the presence of noisy updates. Taken together, our results suggest two routes towards the discovery of neural implementations for credit assignment without weight symmetry: further improvement of local rules so that they perform consistently across architectures and the identification of biological implementations for non-local learning mechanisms.