Get rich quick: exact solutions reveal how unbalanced initializations promote rapid feature learning

While the impressive performance of modern neural networks is often attributed to their capacity to efficiently extract task-relevant features from data, the mechanisms underlying this rich feature learning regime remain elusive, with much of our theoretical understanding stemming from the opposing lazy regime. In this work, we derive exact solutions to a minimal model that transitions between lazy and rich learning, precisely elucidating how unbalanced layer-specific initialization variances and learning rates determine the degree of feature learning. Our analysis reveals that they conspire to influence the learning regime through a set of conserved quantities that constrain and modify the geometry of learning trajectories in parameter and function space. We extend our analysis to more complex linear models with multiple neurons, outputs, and layers and to shallow nonlinear networks with piecewise linear activation functions. In linear networks, rapid feature learning only occurs with balanced initializations, where all layers learn at similar speeds. While in nonlinear networks, unbalanced initializations that promote faster learning in earlier layers can accelerate rich learning. Through a series of experiments, we provide evidence that this unbalanced rich regime drives feature learning in deep finite-width networks, promotes interpretability of early layers in CNNs, reduces the sample complexity of learning hierarchical data, and decreases the time to grokking in modular arithmetic. Our theory motivates further exploration of unbalanced initializations to enhance efficient feature learning.

Pretraining task diversity and the emergence of non-Bayesian in-context learning for regression

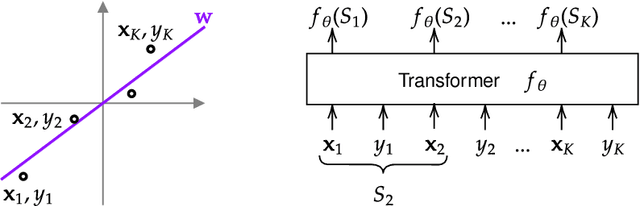
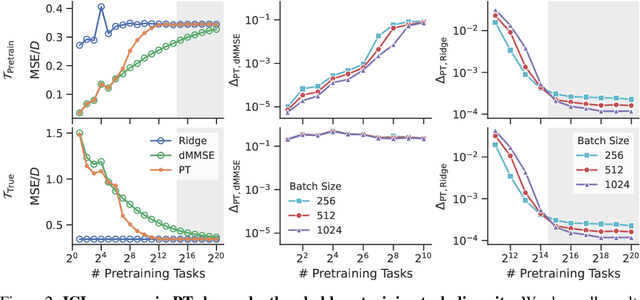
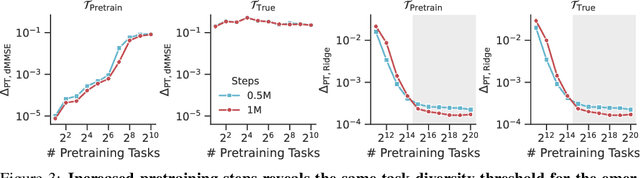
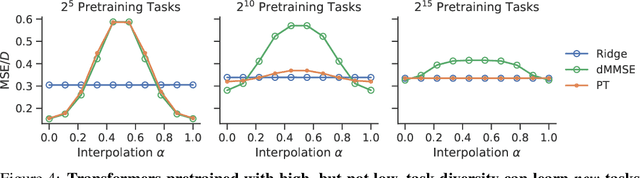
Pretrained transformers exhibit the remarkable ability of in-context learning (ICL): they can learn tasks from just a few examples provided in the prompt without updating any weights. This raises a foundational question: can ICL solve fundamentally $\textit{new}$ tasks that are very different from those seen during pretraining? To probe this question, we examine ICL's performance on linear regression while varying the diversity of tasks in the pretraining dataset. We empirically demonstrate a $\textit{task diversity threshold}$ for the emergence of ICL. Below this threshold, the pretrained transformer cannot solve unseen regression tasks as it behaves like a Bayesian estimator with the $\textit{non-diverse pretraining task distribution}$ as the prior. Beyond this threshold, the transformer significantly outperforms this estimator; its behavior aligns with that of ridge regression, corresponding to a Gaussian prior over $\textit{all tasks}$, including those not seen during pretraining. These results highlight that, when pretrained on data with task diversity greater than the threshold, transformers $\textit{can}$ solve fundamentally new tasks in-context. Importantly, this capability hinges on it deviating from the Bayes optimal estimator with the pretraining distribution as the prior. This study underscores, in a concrete example, the critical role of task diversity, alongside data and model scale, in the emergence of ICL. Code is available at https://github.com/mansheej/icl-task-diversity.

SIXO: Smoothing Inference with Twisted Objectives

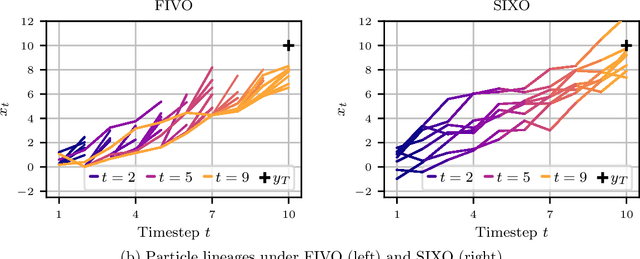
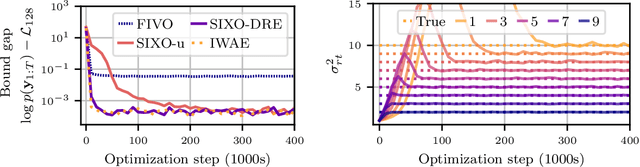
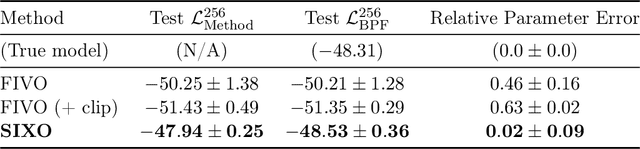
Sequential Monte Carlo (SMC) is an inference algorithm for state space models that approximates the posterior by sampling from a sequence of target distributions. The target distributions are often chosen to be the filtering distributions, but these ignore information from future observations, leading to practical and theoretical limitations in inference and model learning. We introduce SIXO, a method that instead learns targets that approximate the smoothing distributions, incorporating information from all observations. The key idea is to use density ratio estimation to fit functions that warp the filtering distributions into the smoothing distributions. We then use SMC with these learned targets to define a variational objective for model and proposal learning. SIXO yields provably tighter log marginal lower bounds and offers significantly more accurate posterior inferences and parameter estimates in a variety of domains.