Foundation Artificial Intelligence Models for Health Recognition Using Face Photographs (FAHR-Face)

Background: Facial appearance offers a noninvasive window into health. We built FAHR-Face, a foundation model trained on >40 million facial images and fine-tuned it for two distinct tasks: biological age estimation (FAHR-FaceAge) and survival risk prediction (FAHR-FaceSurvival). Methods: FAHR-FaceAge underwent a two-stage, age-balanced fine-tuning on 749,935 public images; FAHR-FaceSurvival was fine-tuned on 34,389 photos of cancer patients. Model robustness (cosmetic surgery, makeup, pose, lighting) and independence (saliency mapping) was tested extensively. Both models were clinically tested in two independent cancer patient datasets with survival analyzed by multivariable Cox models and adjusted for clinical prognostic factors. Findings: For age estimation, FAHR-FaceAge had the lowest mean absolute error of 5.1 years on public datasets, outperforming benchmark models and maintaining accuracy across the full human lifespan. In cancer patients, FAHR-FaceAge outperformed a prior facial age estimation model in survival prognostication. FAHR-FaceSurvival demonstrated robust prediction of mortality, and the highest-risk quartile had more than triple the mortality of the lowest (adjusted hazard ratio 3.22; P<0.001). These findings were validated in the independent cohort and both models showed generalizability across age, sex, race and cancer subgroups. The two algorithms provided distinct, complementary prognostic information; saliency mapping revealed each model relied on distinct facial regions. The combination of FAHR-FaceAge and FAHR-FaceSurvival improved prognostic accuracy. Interpretation: A single foundation model can generate inexpensive, scalable facial biomarkers that capture both biological ageing and disease-related mortality risk. The foundation model enabled effective training using relatively small clinical datasets.

Deep Linear Hawkes Processes

Marked temporal point processes (MTPPs) are used to model sequences of different types of events with irregular arrival times, with broad applications ranging from healthcare and social networks to finance. We address shortcomings in existing point process models by drawing connections between modern deep state-space models (SSMs) and linear Hawkes processes (LHPs), culminating in an MTPP that we call the deep linear Hawkes process (DLHP). The DLHP modifies the linear differential equations in deep SSMs to be stochastic jump differential equations, akin to LHPs. After discretizing, the resulting recurrence can be implemented efficiently using a parallel scan. This brings parallelism and linear scaling to MTPP models. This contrasts with attention-based MTPPs, which scale quadratically, and RNN-based MTPPs, which do not parallelize across the sequence length. We show empirically that DLHPs match or outperform existing models across a broad range of metrics on eight real-world datasets. Our proposed DLHP model is the first instance of the unique architectural capabilities of SSMs being leveraged to construct a new class of MTPP models.

Towards Scalable and Stable Parallelization of Nonlinear RNNs

Conventional nonlinear RNNs are not naturally parallelizable across the sequence length, whereas transformers and linear RNNs are. Lim et al. [2024] therefore tackle parallelized evaluation of nonlinear RNNs by posing it as a fixed point problem, solved with Newton's method. By deriving and applying a parallelized form of Newton's method, they achieve huge speedups over sequential evaluation. However, their approach inherits cubic computational complexity and numerical instability. We tackle these weaknesses. To reduce the computational complexity, we apply quasi-Newton approximations and show they converge comparably to full-Newton, use less memory, and are faster. To stabilize Newton's method, we leverage a connection between Newton's method damped with trust regions and Kalman smoothing. This connection allows us to stabilize Newtons method, per the trust region, while using efficient parallelized Kalman algorithms to retain performance. We compare these methods empirically, and highlight the use cases where each algorithm excels.

Switching Autoregressive Low-rank Tensor Models

An important problem in time-series analysis is modeling systems with time-varying dynamics. Probabilistic models with joint continuous and discrete latent states offer interpretable, efficient, and experimentally useful descriptions of such data. Commonly used models include autoregressive hidden Markov models (ARHMMs) and switching linear dynamical systems (SLDSs), each with its own advantages and disadvantages. ARHMMs permit exact inference and easy parameter estimation, but are parameter intensive when modeling long dependencies, and hence are prone to overfitting. In contrast, SLDSs can capture long-range dependencies in a parameter efficient way through Markovian latent dynamics, but present an intractable likelihood and a challenging parameter estimation task. In this paper, we propose switching autoregressive low-rank tensor (SALT) models, which retain the advantages of both approaches while ameliorating the weaknesses. SALT parameterizes the tensor of an ARHMM with a low-rank factorization to control the number of parameters and allow longer range dependencies without overfitting. We prove theoretical and discuss practical connections between SALT, linear dynamical systems, and SLDSs. We empirically demonstrate quantitative advantages of SALT models on a range of simulated and real prediction tasks, including behavioral and neural datasets. Furthermore, the learned low-rank tensor provides novel insights into temporal dependencies within each discrete state.

Simplified State Space Layers for Sequence Modeling

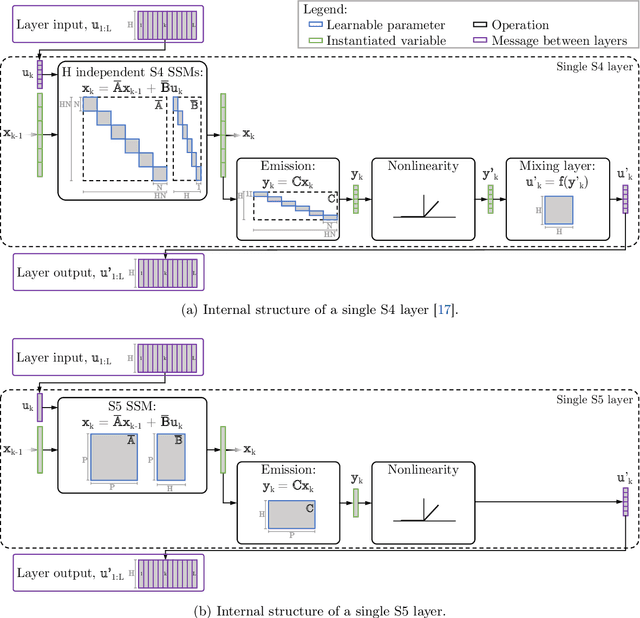
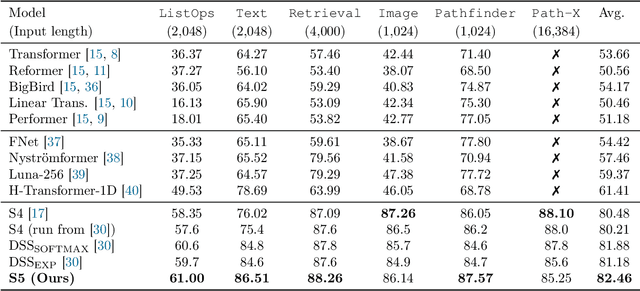
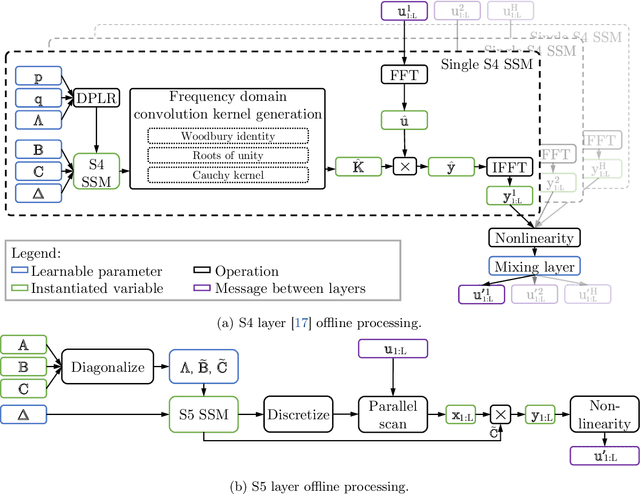
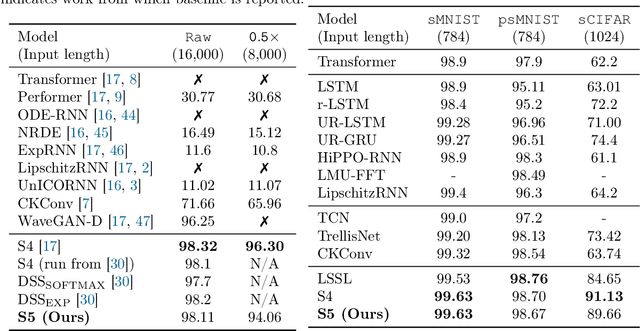
Efficiently modeling long-range dependencies is an important goal in sequence modeling. Recently, models using structured state space sequence (S4) layers achieved state-of-the-art performance on many long-range tasks. The S4 layer combines linear state space models (SSMs) with deep learning techniques and leverages the HiPPO framework for online function approximation to achieve high performance. However, this framework led to architectural constraints and computational difficulties that make the S4 approach complicated to understand and implement. We revisit the idea that closely following the HiPPO framework is necessary for high performance. Specifically, we replace the bank of many independent single-input, single-output (SISO) SSMs the S4 layer uses with one multi-input, multi-output (MIMO) SSM with a reduced latent dimension. The reduced latent dimension of the MIMO system allows for the use of efficient parallel scans which simplify the computations required to apply the S5 layer as a sequence-to-sequence transformation. In addition, we initialize the state matrix of the S5 SSM with an approximation to the HiPPO-LegS matrix used by S4's SSMs and show that this serves as an effective initialization for the MIMO setting. S5 matches S4's performance on long-range tasks, including achieving an average of 82.46% on the suite of Long Range Arena benchmarks compared to S4's 80.48% and the best transformer variant's 61.41%.

SIXO: Smoothing Inference with Twisted Objectives

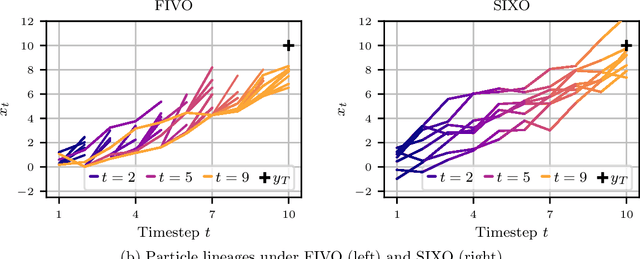
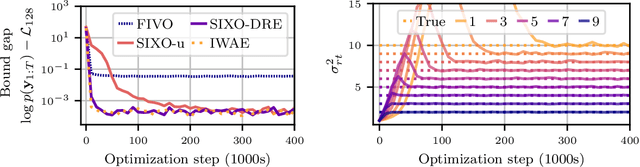
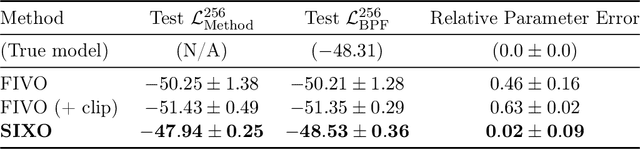
Sequential Monte Carlo (SMC) is an inference algorithm for state space models that approximates the posterior by sampling from a sequence of target distributions. The target distributions are often chosen to be the filtering distributions, but these ignore information from future observations, leading to practical and theoretical limitations in inference and model learning. We introduce SIXO, a method that instead learns targets that approximate the smoothing distributions, incorporating information from all observations. The key idea is to use density ratio estimation to fit functions that warp the filtering distributions into the smoothing distributions. We then use SMC with these learned targets to define a variational objective for model and proposal learning. SIXO yields provably tighter log marginal lower bounds and offers significantly more accurate posterior inferences and parameter estimates in a variety of domains.

Robust Asymmetric Learning in POMDPs

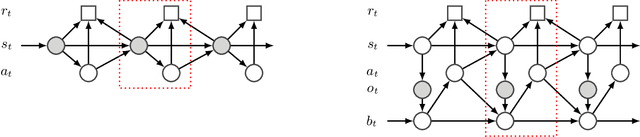
Policies for partially observed Markov decision processes can be efficiently learned by imitating policies for the corresponding fully observed Markov decision processes. Unfortunately, existing approaches for this kind of imitation learning have a serious flaw: the expert does not know what the trainee cannot see, and so may encourage actions that are sub-optimal, even unsafe, under partial information. We derive an objective to instead train the expert to maximize the expected reward of the imitating agent policy, and use it to construct an efficient algorithm, adaptive asymmetric DAgger (A2D), that jointly trains the expert and the agent. We show that A2D produces an expert policy that the agent can safely imitate, in turn outperforming policies learned by imitating a fixed expert.

Planning as Inference in Epidemiological Models

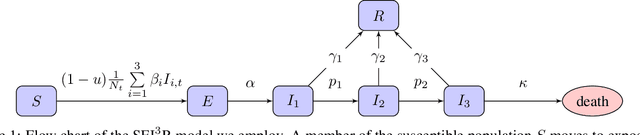
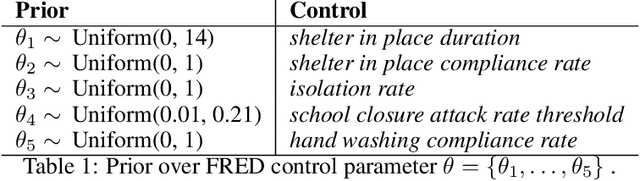
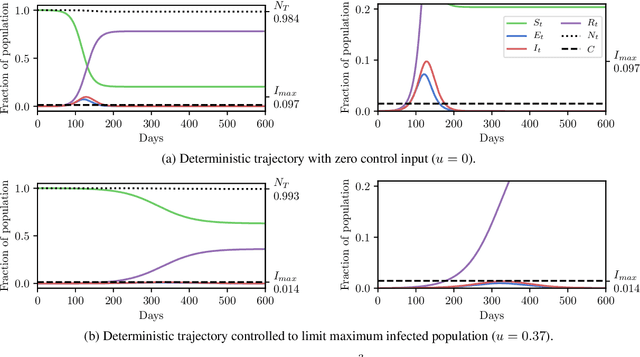
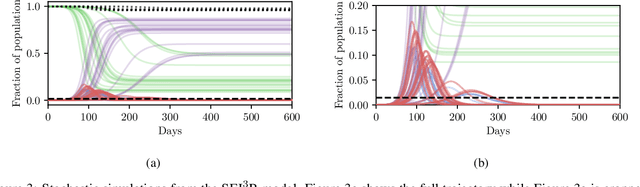
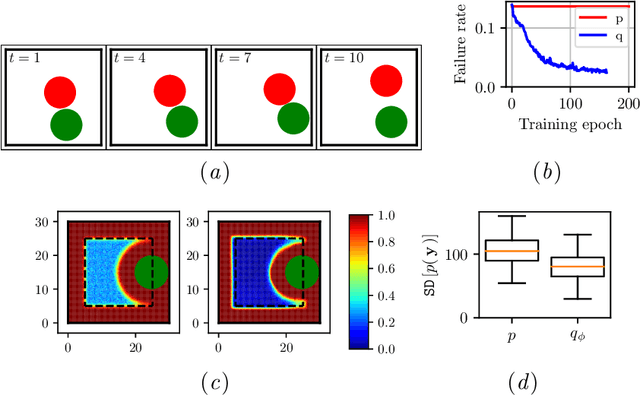
In this work we demonstrate how existing software tools can be used to automate parts of infectious disease-control policy-making via performing inference in existing epidemiological dynamics models. The kind of inference tasks undertaken include computing, for planning purposes, the posterior distribution over putatively controllable, via direct policy-making choices, simulation model parameters that give rise to acceptable disease progression outcomes. Neither the full capabilities of such inference automation software tools nor their utility for planning is widely disseminated at the current time. Timely gains in understanding about these tools and how they can be used may lead to more fine-grained and less economically damaging policy prescriptions, particularly during the current COVID-19 pandemic.

Coping With Simulators That Don't Always Return

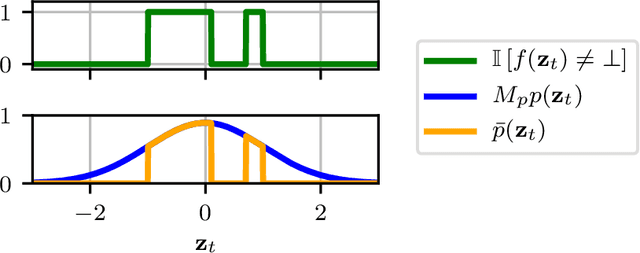
Deterministic models are approximations of reality that are easy to interpret and often easier to build than stochastic alternatives. Unfortunately, as nature is capricious, observational data can never be fully explained by deterministic models in practice. Observation and process noise need to be added to adapt deterministic models to behave stochastically, such that they are capable of explaining and extrapolating from noisy data. We investigate and address computational inefficiencies that arise from adding process noise to deterministic simulators that fail to return for certain inputs; a property we describe as "brittle." We show how to train a conditional normalizing flow to propose perturbations such that the simulator succeeds with high probability, increasing computational efficiency.

The Virtual Patch Clamp: Imputing C. elegans Membrane Potentials from Calcium Imaging

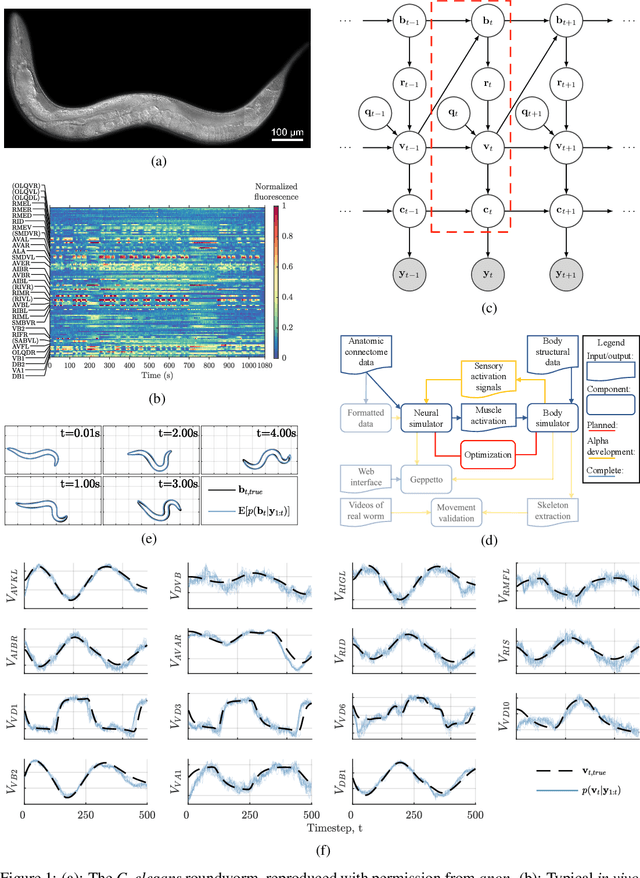
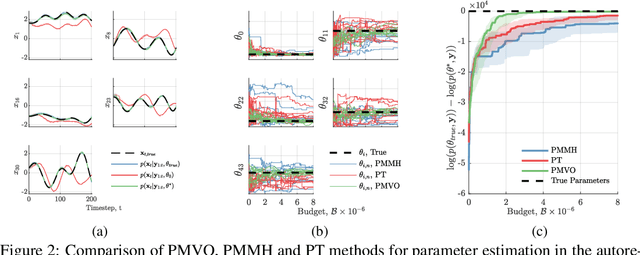
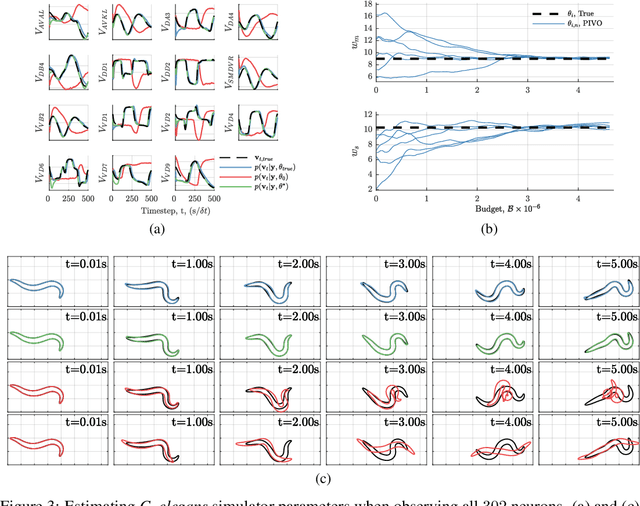
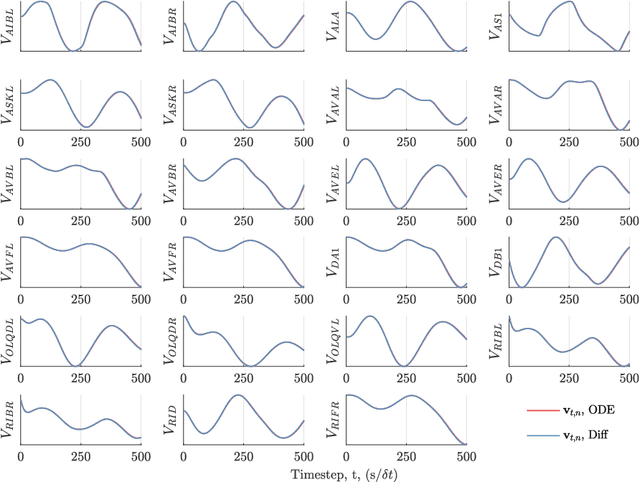
We develop a stochastic whole-brain and body simulator of the nematode roundworm Caenorhabditis elegans (C. elegans) and show that it is sufficiently regularizing to allow imputation of latent membrane potentials from partial calcium fluorescence imaging observations. This is the first attempt we know of to "complete the circle," where an anatomically grounded whole-connectome simulator is used to impute a time-varying "brain" state at single-cell fidelity from covariates that are measurable in practice. The sequential Monte Carlo (SMC) method we employ not only enables imputation of said latent states but also presents a strategy for learning simulator parameters via variational optimization of the noisy model evidence approximation provided by SMC. Our imputation and parameter estimation experiments were conducted on distributed systems using novel implementations of the aforementioned techniques applied to synthetic data of dimension and type representative of that which are measured in laboratories currently.