Deep Linear Hawkes Processes

Marked temporal point processes (MTPPs) are used to model sequences of different types of events with irregular arrival times, with broad applications ranging from healthcare and social networks to finance. We address shortcomings in existing point process models by drawing connections between modern deep state-space models (SSMs) and linear Hawkes processes (LHPs), culminating in an MTPP that we call the deep linear Hawkes process (DLHP). The DLHP modifies the linear differential equations in deep SSMs to be stochastic jump differential equations, akin to LHPs. After discretizing, the resulting recurrence can be implemented efficiently using a parallel scan. This brings parallelism and linear scaling to MTPP models. This contrasts with attention-based MTPPs, which scale quadratically, and RNN-based MTPPs, which do not parallelize across the sequence length. We show empirically that DLHPs match or outperform existing models across a broad range of metrics on eight real-world datasets. Our proposed DLHP model is the first instance of the unique architectural capabilities of SSMs being leveraged to construct a new class of MTPP models.

Adaptive Catalyst Discovery Using Multicriteria Bayesian Optimization with Representation Learning

High-performance catalysts are crucial for sustainable energy conversion and human health. However, the discovery of catalysts faces challenges due to the absence of efficient approaches to navigating vast and high-dimensional structure and composition spaces. In this study, we propose a high-throughput computational catalyst screening approach integrating density functional theory (DFT) and Bayesian Optimization (BO). Within the BO framework, we propose an uncertainty-aware atomistic machine learning model, UPNet, which enables automated representation learning directly from high-dimensional catalyst structures and achieves principled uncertainty quantification. Utilizing a constrained expected improvement acquisition function, our BO framework simultaneously considers multiple evaluation criteria. Using the proposed methods, we explore catalyst discovery for the CO2 reduction reaction. The results demonstrate that our approach achieves high prediction accuracy, facilitates interpretable feature extraction, and enables multicriteria design optimization, leading to significant reduction of computing power and time (10x reduction of required DFT calculations) in high-performance catalyst discovery.

Probabilistic Modeling for Sequences of Sets in Continuous-Time

Neural marked temporal point processes have been a valuable addition to the existing toolbox of statistical parametric models for continuous-time event data. These models are useful for sequences where each event is associated with a single item (a single type of event or a "mark") -- but such models are not suited for the practical situation where each event is associated with a set of items. In this work, we develop a general framework for modeling set-valued data in continuous-time, compatible with any intensity-based recurrent neural point process model. In addition, we develop inference methods that can use such models to answer probabilistic queries such as "the probability of item $A$ being observed before item $B$," conditioned on sequence history. Computing exact answers for such queries is generally intractable for neural models due to both the continuous-time nature of the problem setting and the combinatorially-large space of potential outcomes for each event. To address this, we develop a class of importance sampling methods for querying with set-based sequences and demonstrate orders-of-magnitude improvements in efficiency over direct sampling via systematic experiments with four real-world datasets. We also illustrate how to use this framework to perform model selection using likelihoods that do not involve one-step-ahead prediction.

Probabilistic Querying of Continuous-Time Event Sequences

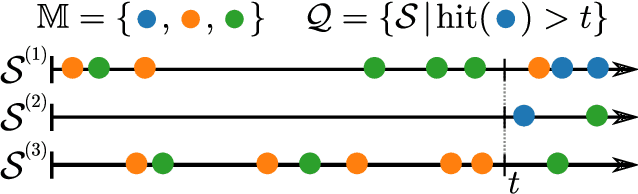
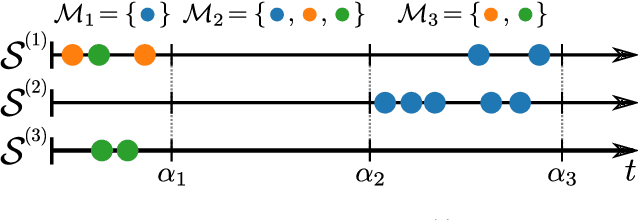
Continuous-time event sequences, i.e., sequences consisting of continuous time stamps and associated event types ("marks"), are an important type of sequential data with many applications, e.g., in clinical medicine or user behavior modeling. Since these data are typically modeled autoregressively (e.g., using neural Hawkes processes or their classical counterparts), it is natural to ask questions about future scenarios such as "what kind of event will occur next" or "will an event of type $A$ occur before one of type $B$". Unfortunately, some of these queries are notoriously hard to address since current methods are limited to naive simulation, which can be highly inefficient. This paper introduces a new typology of query types and a framework for addressing them using importance sampling. Example queries include predicting the $n^\text{th}$ event type in a sequence and the hitting time distribution of one or more event types. We also leverage these findings further to be applicable for estimating general "$A$ before $B$" type of queries. We prove theoretically that our estimation method is effectively always better than naive simulation and show empirically based on three real-world datasets that it is on average 1,000 times more efficient than existing approaches.