On the Efficient Marginalization of Probabilistic Sequence Models

Real-world data often exhibits sequential dependence, across diverse domains such as human behavior, medicine, finance, and climate modeling. Probabilistic methods capture the inherent uncertainty associated with prediction in these contexts, with autoregressive models being especially prominent. This dissertation focuses on using autoregressive models to answer complex probabilistic queries that go beyond single-step prediction, such as the timing of future events or the likelihood of a specific event occurring before another. In particular, we develop a broad class of novel and efficient approximation techniques for marginalization in sequential models that are model-agnostic. These techniques rely solely on access to and sampling from next-step conditional distributions of a pre-trained autoregressive model, including both traditional parametric models as well as more recent neural autoregressive models. Specific approaches are presented for discrete sequential models, for marked temporal point processes, and for stochastic jump processes, each tailored to a well-defined class of informative, long-range probabilistic queries.

Probabilistic Modeling for Sequences of Sets in Continuous-Time

Neural marked temporal point processes have been a valuable addition to the existing toolbox of statistical parametric models for continuous-time event data. These models are useful for sequences where each event is associated with a single item (a single type of event or a "mark") -- but such models are not suited for the practical situation where each event is associated with a set of items. In this work, we develop a general framework for modeling set-valued data in continuous-time, compatible with any intensity-based recurrent neural point process model. In addition, we develop inference methods that can use such models to answer probabilistic queries such as "the probability of item $A$ being observed before item $B$," conditioned on sequence history. Computing exact answers for such queries is generally intractable for neural models due to both the continuous-time nature of the problem setting and the combinatorially-large space of potential outcomes for each event. To address this, we develop a class of importance sampling methods for querying with set-based sequences and demonstrate orders-of-magnitude improvements in efficiency over direct sampling via systematic experiments with four real-world datasets. We also illustrate how to use this framework to perform model selection using likelihoods that do not involve one-step-ahead prediction.

Bayesian Online Learning for Consensus Prediction

Given a pre-trained classifier and multiple human experts, we investigate the task of online classification where model predictions are provided for free but querying humans incurs a cost. In this practical but under-explored setting, oracle ground truth is not available. Instead, the prediction target is defined as the consensus vote of all experts. Given that querying full consensus can be costly, we propose a general framework for online Bayesian consensus estimation, leveraging properties of the multivariate hypergeometric distribution. Based on this framework, we propose a family of methods that dynamically estimate expert consensus from partial feedback by producing a posterior over expert and model beliefs. Analyzing this posterior induces an interpretable trade-off between querying cost and classification performance. We demonstrate the efficacy of our framework against a variety of baselines on CIFAR-10H and ImageNet-16H, two large-scale crowdsourced datasets.

Understanding Pathologies of Deep Heteroskedastic Regression

Several recent studies have reported negative results when using heteroskedastic neural regression models to model real-world data. In particular, for overparameterized models, the mean and variance networks are powerful enough to either fit every single data point (while shrinking the predicted variances to zero), or to learn a constant prediction with an output variance exactly matching every predicted residual (i.e., explaining the targets as pure noise). This paper studies these difficulties from the perspective of statistical physics. We show that the observed instabilities are not specific to any neural network architecture but are already present in a field theory of an overparameterized conditional Gaussian likelihood model. Under light assumptions, we derive a nonparametric free energy that can be solved numerically. The resulting solutions show excellent qualitative agreement with empirical model fits on real-world data and, in particular, prove the existence of phase transitions, i.e., abrupt, qualitative differences in the behaviors of the regressors upon varying the regularization strengths on the two networks. Our work thus provides a theoretical explanation for the necessity to carefully regularize heteroskedastic regression models. Moreover, the insights from our theory suggest a scheme for optimizing this regularization which is quadratically more efficient than the naive approach.

Probabilistic Querying of Continuous-Time Event Sequences

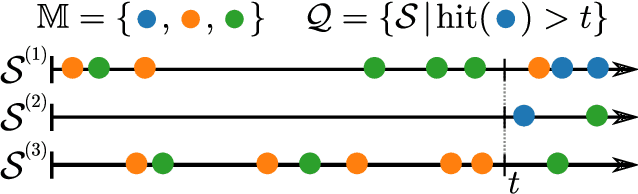
Continuous-time event sequences, i.e., sequences consisting of continuous time stamps and associated event types ("marks"), are an important type of sequential data with many applications, e.g., in clinical medicine or user behavior modeling. Since these data are typically modeled autoregressively (e.g., using neural Hawkes processes or their classical counterparts), it is natural to ask questions about future scenarios such as "what kind of event will occur next" or "will an event of type $A$ occur before one of type $B$". Unfortunately, some of these queries are notoriously hard to address since current methods are limited to naive simulation, which can be highly inefficient. This paper introduces a new typology of query types and a framework for addressing them using importance sampling. Example queries include predicting the $n^\text{th}$ event type in a sequence and the hitting time distribution of one or more event types. We also leverage these findings further to be applicable for estimating general "$A$ before $B$" type of queries. We prove theoretically that our estimation method is effectively always better than naive simulation and show empirically based on three real-world datasets that it is on average 1,000 times more efficient than existing approaches.

Predictive Querying for Autoregressive Neural Sequence Models

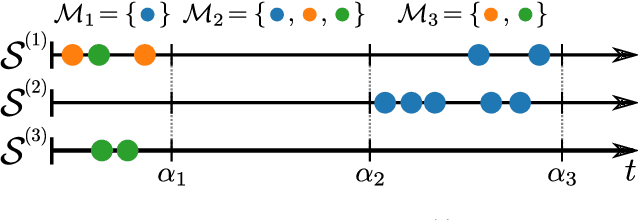
In reasoning about sequential events it is natural to pose probabilistic queries such as "when will event A occur next" or "what is the probability of A occurring before B", with applications in areas such as user modeling, medicine, and finance. However, with machine learning shifting towards neural autoregressive models such as RNNs and transformers, probabilistic querying has been largely restricted to simple cases such as next-event prediction. This is in part due to the fact that future querying involves marginalization over large path spaces, which is not straightforward to do efficiently in such models. In this paper we introduce a general typology for predictive queries in neural autoregressive sequence models and show that such queries can be systematically represented by sets of elementary building blocks. We leverage this typology to develop new query estimation methods based on beam search, importance sampling, and hybrids. Across four large-scale sequence datasets from different application domains, as well as for the GPT-2 language model, we demonstrate the ability to make query answering tractable for arbitrary queries in exponentially-large predictive path-spaces, and find clear differences in cost-accuracy tradeoffs between search and sampling methods.

Structured Stochastic Gradient MCMC

Stochastic gradient Markov chain Monte Carlo (SGMCMC) is considered the gold standard for Bayesian inference in large-scale models, such as Bayesian neural networks. Since practitioners face speed versus accuracy tradeoffs in these models, variational inference (VI) is often the preferable option. Unfortunately, VI makes strong assumptions on both the factorization and functional form of the posterior. In this work, we propose a new non-parametric variational approximation that makes no assumptions about the approximate posterior's functional form and allows practitioners to specify the exact dependencies the algorithm should respect or break. The approach relies on a new Langevin-type algorithm that operates on a modified energy function, where parts of the latent variables are averaged over samples from earlier iterations of the Markov chain. This way, statistical dependencies can be broken in a controlled way, allowing the chain to mix faster. This scheme can be further modified in a ''dropout'' manner, leading to even more scalability. By implementing the scheme on a ResNet-20 architecture, we obtain better predictive likelihoods and larger effective sample sizes than full SGMCMC.

Variational Beam Search for Online Learning with Distribution Shifts

We consider the problem of online learning in the presence of sudden distribution shifts as frequently encountered in applications such as autonomous navigation. Distribution shifts require constant performance monitoring and re-training. They may also be hard to detect and can lead to a slow but steady degradation in model performance. To address this problem we propose a new Bayesian meta-algorithm that can both (i) make inferences about subtle distribution shifts based on minimal sequential observations and (ii) accordingly adapt a model in an online fashion. The approach uses beam search over multiple change point hypotheses to perform inference on a hierarchical sequential latent variable modeling framework. Our proposed approach is model-agnostic, applicable to both supervised and unsupervised learning, and yields significant improvements over state-of-the-art Bayesian online learning approaches.

User-Dependent Neural Sequence Models for Continuous-Time Event Data

Continuous-time event data are common in applications such as individual behavior data, financial transactions, and medical health records. Modeling such data can be very challenging, in particular for applications with many different types of events, since it requires a model to predict the event types as well as the time of occurrence. Recurrent neural networks that parameterize time-varying intensity functions are the current state-of-the-art for predictive modeling with such data. These models typically assume that all event sequences come from the same data distribution. However, in many applications event sequences are generated by different sources, or users, and their characteristics can be very different. In this paper, we extend the broad class of neural marked point process models to mixtures of latent embeddings, where each mixture component models the characteristic traits of a given user. Our approach relies on augmenting these models with a latent variable that encodes user characteristics, represented by a mixture model over user behavior that is trained via amortized variational inference. We evaluate our methods on four large real-world datasets and demonstrate systematic improvements from our approach over existing work for a variety of predictive metrics such as log-likelihood, next event ranking, and source-of-sequence identification.

Large Scale Multi-Actor Generative Dialog Modeling

Non-goal oriented dialog agents (i.e. chatbots) aim to produce varying and engaging conversations with a user; however, they typically exhibit either inconsistent personality across conversations or the average personality of all users. This paper addresses these issues by controlling an agent's persona upon generation via conditioning on prior conversations of a target actor. In doing so, we are able to utilize more abstract patterns within a person's speech and better emulate them in generated responses. This work introduces the Generative Conversation Control model, an augmented and fine-tuned GPT-2 language model that conditions on past reference conversations to probabilistically model multi-turn conversations in the actor's persona. We introduce an accompanying data collection procedure to obtain 10.3M conversations from 6 months worth of Reddit comments. We demonstrate that scaling model sizes from 117M to 8.3B parameters yields an improvement from 23.14 to 13.14 perplexity on 1.7M held out Reddit conversations. Increasing model scale yielded similar improvements in human evaluations that measure preference of model samples to the held out target distribution in terms of realism (31% increased to 37% preference), style matching (37% to 42%), grammar and content quality (29% to 42%), and conversation coherency (32% to 40%). We find that conditionally modeling past conversations improves perplexity by 0.47 in automatic evaluations. Through human trials we identify positive trends between conditional modeling and style matching and outline steps to further improve persona control.