Birdie: Advancing State Space Models with Reward-Driven Objectives and Curricula

Efficient state space models (SSMs), such as linear recurrent neural networks and linear attention variants, offer computational advantages over Transformers but struggle with tasks requiring long-range in-context retrieval-like text copying, associative recall, and question answering over long contexts. Previous efforts to address these challenges have focused on architectural modifications, often reintroducing computational inefficiencies. In this paper, we propose a novel training procedure, Birdie, that significantly enhances the in-context retrieval capabilities of SSMs without altering their architecture. Our approach combines bidirectional input processing with dynamic mixtures of specialized pre-training objectives, optimized via reinforcement learning. We introduce a new bidirectional SSM architecture that seamlessly transitions from bidirectional context processing to causal generation. Experimental evaluations demonstrate that Birdie markedly improves performance on retrieval-intensive tasks such as multi-number phone book lookup, long paragraph question-answering, and infilling. This narrows the performance gap with Transformers, while retaining computational efficiency. Our findings highlight the importance of training procedures in leveraging the fixed-state capacity of SSMs, offering a new direction to advance their capabilities. All code and pre-trained models are available at https://www.github.com/samblouir/birdie, with support for JAX and PyTorch.

Towards Scalable and Stable Parallelization of Nonlinear RNNs

Conventional nonlinear RNNs are not naturally parallelizable across the sequence length, whereas transformers and linear RNNs are. Lim et al. [2024] therefore tackle parallelized evaluation of nonlinear RNNs by posing it as a fixed point problem, solved with Newton's method. By deriving and applying a parallelized form of Newton's method, they achieve huge speedups over sequential evaluation. However, their approach inherits cubic computational complexity and numerical instability. We tackle these weaknesses. To reduce the computational complexity, we apply quasi-Newton approximations and show they converge comparably to full-Newton, use less memory, and are faster. To stabilize Newton's method, we leverage a connection between Newton's method damped with trust regions and Kalman smoothing. This connection allows us to stabilize Newtons method, per the trust region, while using efficient parallelized Kalman algorithms to retain performance. We compare these methods empirically, and highlight the use cases where each algorithm excels.

Towards a theory of learning dynamics in deep state space models

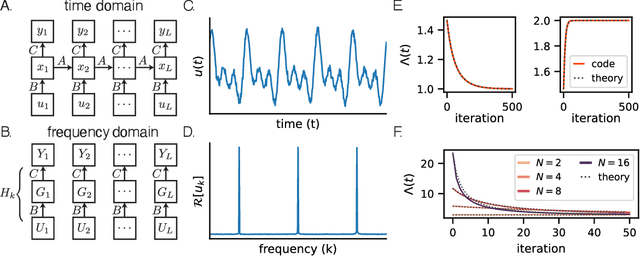
State space models (SSMs) have shown remarkable empirical performance on many long sequence modeling tasks, but a theoretical understanding of these models is still lacking. In this work, we study the learning dynamics of linear SSMs to understand how covariance structure in data, latent state size, and initialization affect the evolution of parameters throughout learning with gradient descent. We show that focusing on the learning dynamics in the frequency domain affords analytical solutions under mild assumptions, and we establish a link between one-dimensional SSMs and the dynamics of deep linear feed-forward networks. Finally, we analyze how latent state over-parameterization affects convergence time and describe future work in extending our results to the study of deep SSMs with nonlinear connections. This work is a step toward a theory of learning dynamics in deep state space models.

State-Free Inference of State-Space Models: The Transfer Function Approach

We approach designing a state-space model for deep learning applications through its dual representation, the transfer function, and uncover a highly efficient sequence parallel inference algorithm that is state-free: unlike other proposed algorithms, state-free inference does not incur any significant memory or computational cost with an increase in state size. We achieve this using properties of the proposed frequency domain transfer function parametrization, which enables direct computation of its corresponding convolutional kernel's spectrum via a single Fast Fourier Transform. Our experimental results across multiple sequence lengths and state sizes illustrates, on average, a 35% training speed improvement over S4 layers -- parametrized in time-domain -- on the Long Range Arena benchmark, while delivering state-of-the-art downstream performances over other attention-free approaches. Moreover, we report improved perplexity in language modeling over a long convolutional Hyena baseline, by simply introducing our transfer function parametrization. Our code is available at https://github.com/ruke1ire/RTF.

Convolutional State Space Models for Long-Range Spatiotemporal Modeling

Effectively modeling long spatiotemporal sequences is challenging due to the need to model complex spatial correlations and long-range temporal dependencies simultaneously. ConvLSTMs attempt to address this by updating tensor-valued states with recurrent neural networks, but their sequential computation makes them slow to train. In contrast, Transformers can process an entire spatiotemporal sequence, compressed into tokens, in parallel. However, the cost of attention scales quadratically in length, limiting their scalability to longer sequences. Here, we address the challenges of prior methods and introduce convolutional state space models (ConvSSM) that combine the tensor modeling ideas of ConvLSTM with the long sequence modeling approaches of state space methods such as S4 and S5. First, we demonstrate how parallel scans can be applied to convolutional recurrences to achieve subquadratic parallelization and fast autoregressive generation. We then establish an equivalence between the dynamics of ConvSSMs and SSMs, which motivates parameterization and initialization strategies for modeling long-range dependencies. The result is ConvS5, an efficient ConvSSM variant for long-range spatiotemporal modeling. ConvS5 significantly outperforms Transformers and ConvLSTM on a long horizon Moving-MNIST experiment while training 3X faster than ConvLSTM and generating samples 400X faster than Transformers. In addition, ConvS5 matches or exceeds the performance of state-of-the-art methods on challenging DMLab, Minecraft and Habitat prediction benchmarks and enables new directions for modeling long spatiotemporal sequences.

Simplified State Space Layers for Sequence Modeling

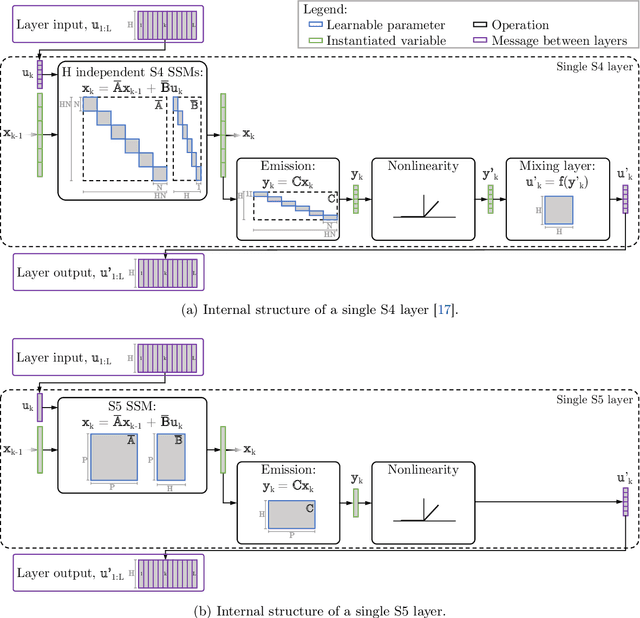
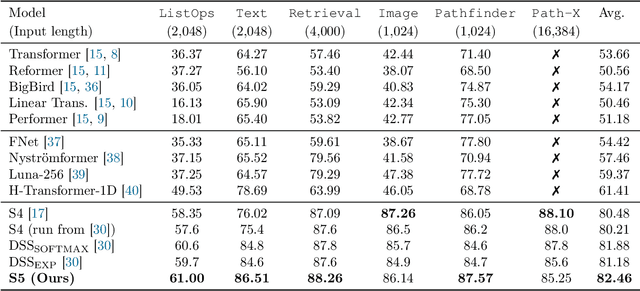
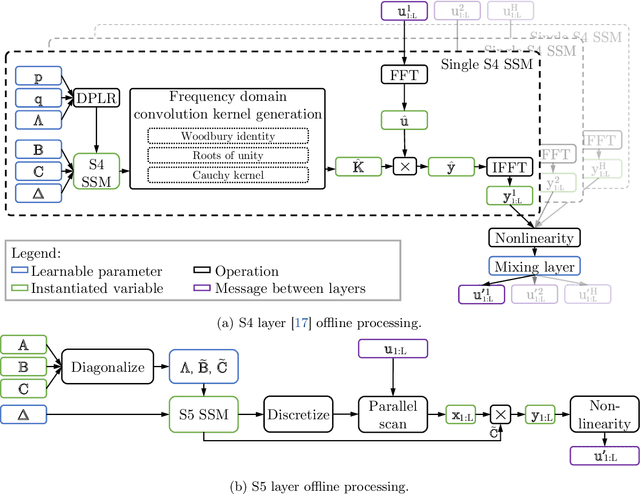
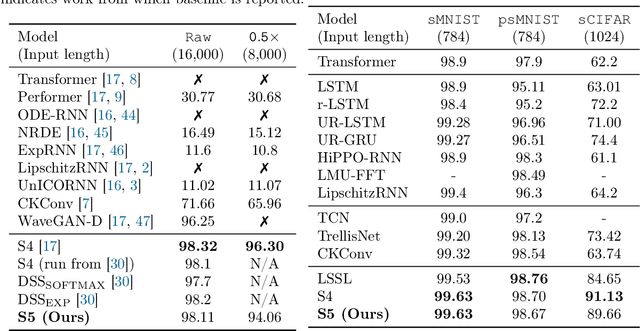
Efficiently modeling long-range dependencies is an important goal in sequence modeling. Recently, models using structured state space sequence (S4) layers achieved state-of-the-art performance on many long-range tasks. The S4 layer combines linear state space models (SSMs) with deep learning techniques and leverages the HiPPO framework for online function approximation to achieve high performance. However, this framework led to architectural constraints and computational difficulties that make the S4 approach complicated to understand and implement. We revisit the idea that closely following the HiPPO framework is necessary for high performance. Specifically, we replace the bank of many independent single-input, single-output (SISO) SSMs the S4 layer uses with one multi-input, multi-output (MIMO) SSM with a reduced latent dimension. The reduced latent dimension of the MIMO system allows for the use of efficient parallel scans which simplify the computations required to apply the S5 layer as a sequence-to-sequence transformation. In addition, we initialize the state matrix of the S5 SSM with an approximation to the HiPPO-LegS matrix used by S4's SSMs and show that this serves as an effective initialization for the MIMO setting. S5 matches S4's performance on long-range tasks, including achieving an average of 82.46% on the suite of Long Range Arena benchmarks compared to S4's 80.48% and the best transformer variant's 61.41%.

Reverse engineering recurrent neural networks with Jacobian switching linear dynamical systems

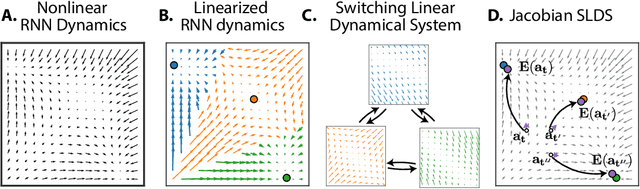
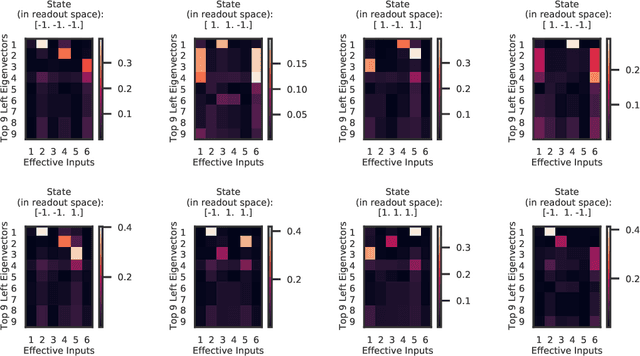
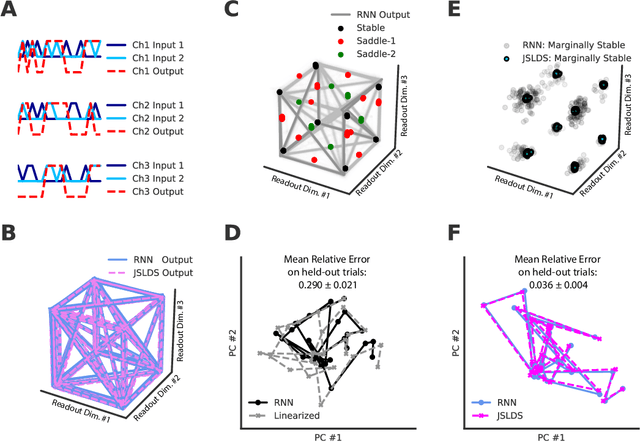
Recurrent neural networks (RNNs) are powerful models for processing time-series data, but it remains challenging to understand how they function. Improving this understanding is of substantial interest to both the machine learning and neuroscience communities. The framework of reverse engineering a trained RNN by linearizing around its fixed points has provided insight, but the approach has significant challenges. These include difficulty choosing which fixed point to expand around when studying RNN dynamics and error accumulation when reconstructing the nonlinear dynamics with the linearized dynamics. We present a new model that overcomes these limitations by co-training an RNN with a novel switching linear dynamical system (SLDS) formulation. A first-order Taylor series expansion of the co-trained RNN and an auxiliary function trained to pick out the RNN's fixed points govern the SLDS dynamics. The results are a trained SLDS variant that closely approximates the RNN, an auxiliary function that can produce a fixed point for each point in state-space, and a trained nonlinear RNN whose dynamics have been regularized such that its first-order terms perform the computation, if possible. This model removes the post-training fixed point optimization and allows us to unambiguously study the learned dynamics of the SLDS at any point in state-space. It also generalizes SLDS models to continuous manifolds of switching points while sharing parameters across switches. We validate the utility of the model on two synthetic tasks relevant to previous work reverse engineering RNNs. We then show that our model can be used as a drop-in in more complex architectures, such as LFADS, and apply this LFADS hybrid to analyze single-trial spiking activity from the motor system of a non-human primate.