Towards a theory of learning dynamics in deep state space models

State space models (SSMs) have shown remarkable empirical performance on many long sequence modeling tasks, but a theoretical understanding of these models is still lacking. In this work, we study the learning dynamics of linear SSMs to understand how covariance structure in data, latent state size, and initialization affect the evolution of parameters throughout learning with gradient descent. We show that focusing on the learning dynamics in the frequency domain affords analytical solutions under mild assumptions, and we establish a link between one-dimensional SSMs and the dynamics of deep linear feed-forward networks. Finally, we analyze how latent state over-parameterization affects convergence time and describe future work in extending our results to the study of deep SSMs with nonlinear connections. This work is a step toward a theory of learning dynamics in deep state space models.

LoRA Learns Less and Forgets Less

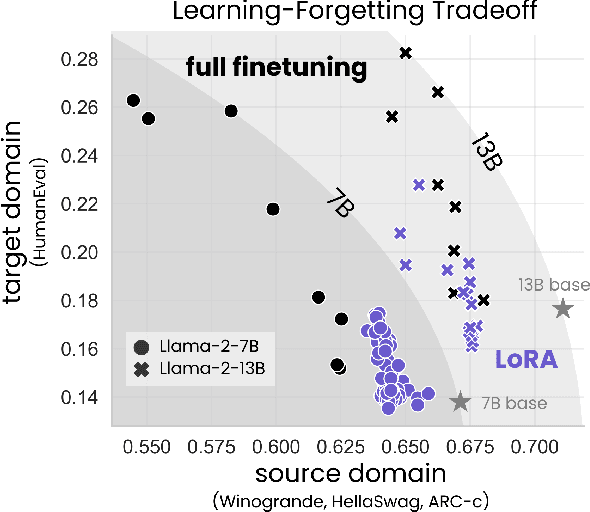
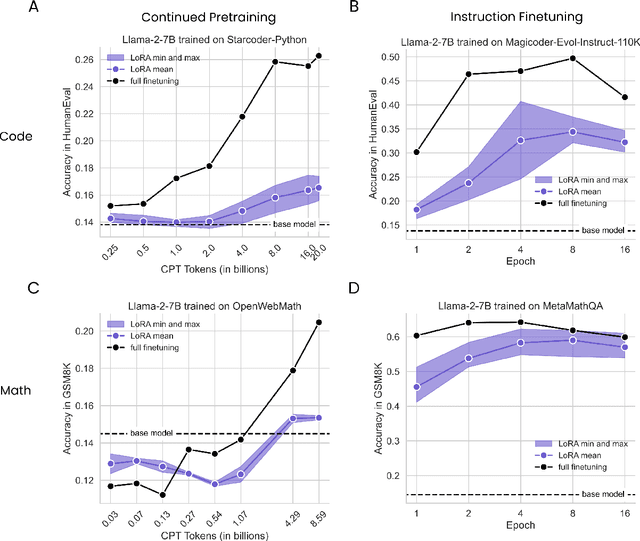
Low-Rank Adaptation (LoRA) is a widely-used parameter-efficient finetuning method for large language models. LoRA saves memory by training only low rank perturbations to selected weight matrices. In this work, we compare the performance of LoRA and full finetuning on two target domains, programming and mathematics. We consider both the instruction finetuning ($\approx$100K prompt-response pairs) and continued pretraining ($\approx$10B unstructured tokens) data regimes. Our results show that, in most settings, LoRA substantially underperforms full finetuning. Nevertheless, LoRA exhibits a desirable form of regularization: it better maintains the base model's performance on tasks outside the target domain. We show that LoRA provides stronger regularization compared to common techniques such as weight decay and dropout; it also helps maintain more diverse generations. We show that full finetuning learns perturbations with a rank that is 10-100X greater than typical LoRA configurations, possibly explaining some of the reported gaps. We conclude by proposing best practices for finetuning with LoRA.

Bias-Free Scalable Gaussian Processes via Randomized Truncations

Scalable Gaussian Process methods are computationally attractive, yet introduce modeling biases that require rigorous study. This paper analyzes two common techniques: early truncated conjugate gradients (CG) and random Fourier features (RFF). We find that both methods introduce a systematic bias on the learned hyperparameters: CG tends to underfit while RFF tends to overfit. We address these issues using randomized truncation estimators that eliminate bias in exchange for increased variance. In the case of RFF, we show that the bias-to-variance conversion is indeed a trade-off: the additional variance proves detrimental to optimization. However, in the case of CG, our unbiased learning procedure meaningfully outperforms its biased counterpart with minimal additional computation.