LoRA Learns Less and Forgets Less

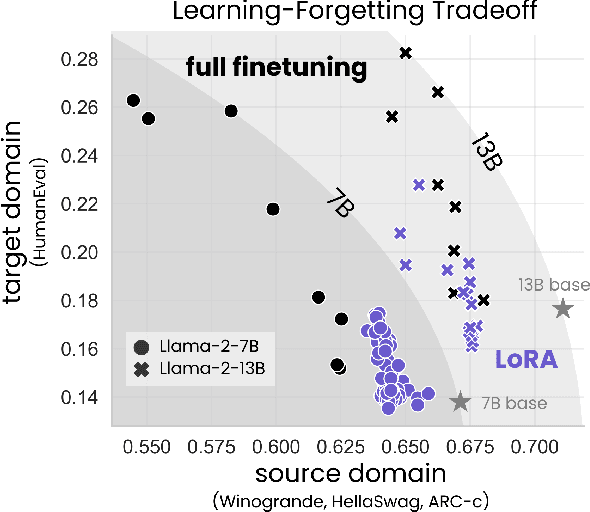
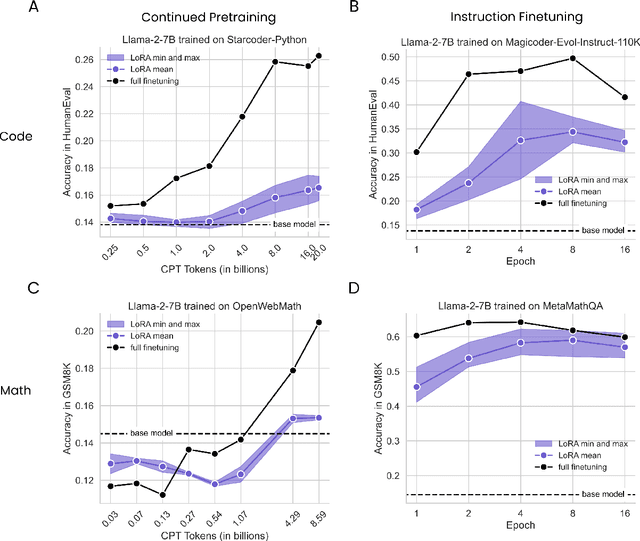
Low-Rank Adaptation (LoRA) is a widely-used parameter-efficient finetuning method for large language models. LoRA saves memory by training only low rank perturbations to selected weight matrices. In this work, we compare the performance of LoRA and full finetuning on two target domains, programming and mathematics. We consider both the instruction finetuning ($\approx$100K prompt-response pairs) and continued pretraining ($\approx$10B unstructured tokens) data regimes. Our results show that, in most settings, LoRA substantially underperforms full finetuning. Nevertheless, LoRA exhibits a desirable form of regularization: it better maintains the base model's performance on tasks outside the target domain. We show that LoRA provides stronger regularization compared to common techniques such as weight decay and dropout; it also helps maintain more diverse generations. We show that full finetuning learns perturbations with a rank that is 10-100X greater than typical LoRA configurations, possibly explaining some of the reported gaps. We conclude by proposing best practices for finetuning with LoRA.

LQ-LoRA: Low-rank Plus Quantized Matrix Decomposition for Efficient Language Model Finetuning

We propose a simple approach for memory-efficient adaptation of pretrained language models. Our approach uses an iterative algorithm to decompose each pretrained matrix into a high-precision low-rank component and a memory-efficient quantized component. During finetuning, the quantized component remains fixed and only the low-rank component is updated. We present an integer linear programming formulation of the quantization component which enables dynamic configuration of quantization parameters (e.g., bit-width, block size) for each matrix given an overall target memory budget. We further explore a data-aware version of the algorithm which uses an approximation of the Fisher information matrix to weight the reconstruction objective during matrix decomposition. Experiments on adapting RoBERTa and LLaMA-2 (7B and 70B) demonstrate that our low-rank plus quantized matrix decomposition approach (LQ-LoRA) outperforms strong QLoRA and GPTQ-LoRA baselines and moreover enables more aggressive quantization. For example, on the OpenAssistant benchmark LQ-LoRA is able to learn a 2.5-bit LLaMA-2 model that is competitive with a model finetuned with 4-bit QLoRA. When finetuned on a language modeling calibration dataset, LQ-LoRA can also be used for model compression; in this setting our 2.75-bit LLaMA-2-70B model (which has 2.85 bits on average when including the low-rank components and requires 27GB of GPU memory) is competitive with the original model in full precision.

Learning to Grow Pretrained Models for Efficient Transformer Training

Scaling transformers has led to significant breakthroughs in many domains, leading to a paradigm in which larger versions of existing models are trained and released on a periodic basis. New instances of such models are typically trained completely from scratch, despite the fact that they are often just scaled-up versions of their smaller counterparts. How can we use the implicit knowledge in the parameters of smaller, extant models to enable faster training of newer, larger models? This paper describes an approach for accelerating transformer training by learning to grow pretrained transformers, where we learn to linearly map the parameters of the smaller model to initialize the larger model. For tractable learning, we factorize the linear transformation as a composition of (linear) width- and depth-growth operators, and further employ a Kronecker factorization of these growth operators to encode architectural knowledge. Extensive experiments across both language and vision transformers demonstrate that our learned Linear Growth Operator (LiGO) can save up to 50% computational cost of training from scratch, while also consistently outperforming strong baselines that also reuse smaller pretrained models to initialize larger models.

Federated Learning as Variational Inference: A Scalable Expectation Propagation Approach

The canonical formulation of federated learning treats it as a distributed optimization problem where the model parameters are optimized against a global loss function that decomposes across client loss functions. A recent alternative formulation instead treats federated learning as a distributed inference problem, where the goal is to infer a global posterior from partitioned client data (Al-Shedivat et al., 2021). This paper extends the inference view and describes a variational inference formulation of federated learning where the goal is to find a global variational posterior that well-approximates the true posterior. This naturally motivates an expectation propagation approach to federated learning (FedEP), where approximations to the global posterior are iteratively refined through probabilistic message-passing between the central server and the clients. We conduct an extensive empirical study across various algorithmic considerations and describe practical strategies for scaling up expectation propagation to the modern federated setting. We apply FedEP on standard federated learning benchmarks and find that it outperforms strong baselines in terms of both convergence speed and accuracy.