Scaling Laws for Precision

Low precision training and inference affect both the quality and cost of language models, but current scaling laws do not account for this. In this work, we devise "precision-aware" scaling laws for both training and inference. We propose that training in lower precision reduces the model's "effective parameter count," allowing us to predict the additional loss incurred from training in low precision and post-train quantization. For inference, we find that the degradation introduced by post-training quantization increases as models are trained on more data, eventually making additional pretraining data actively harmful. For training, our scaling laws allow us to predict the loss of a model with different parts in different precisions, and suggest that training larger models in lower precision may be compute optimal. We unify the scaling laws for post and pretraining quantization to arrive at a single functional form that predicts degradation from training and inference in varied precisions. We fit on over 465 pretraining runs and validate our predictions on model sizes up to 1.7B parameters trained on up to 26B tokens.

Critique-out-Loud Reward Models

Traditionally, reward models used for reinforcement learning from human feedback (RLHF) are trained to directly predict preference scores without leveraging the generation capabilities of the underlying large language model (LLM). This limits the capabilities of reward models as they must reason implicitly about the quality of a response, i.e., preference modeling must be performed in a single forward pass through the model. To enable reward models to reason explicitly about the quality of a response, we introduce Critique-out-Loud (CLoud) reward models. CLoud reward models operate by first generating a natural language critique of the assistant's response that is then used to predict a scalar reward for the quality of the response. We demonstrate the success of CLoud reward models for both Llama-3-8B and 70B base models: compared to classic reward models CLoud reward models improve pairwise preference classification accuracy on RewardBench by 4.65 and 5.84 percentage points for the 8B and 70B base models respectively. Furthermore, CLoud reward models lead to a Pareto improvement for win rate on ArenaHard when used as the scoring model for Best-of-N. Finally, we explore how to exploit the dynamic inference compute capabilities of CLoud reward models by performing self-consistency decoding for reward prediction.

Does your data spark joy? Performance gains from domain upsampling at the end of training

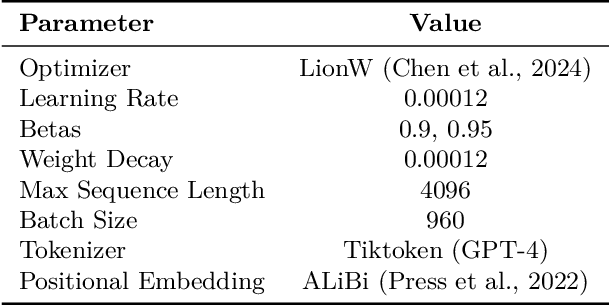
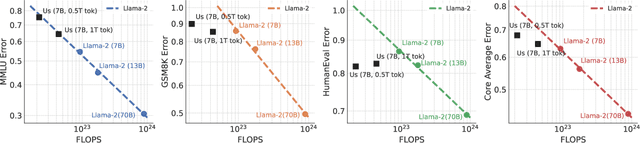
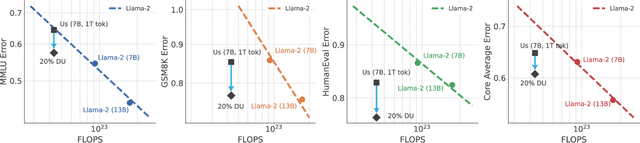
Pretraining datasets for large language models (LLMs) have grown to trillions of tokens composed of large amounts of CommonCrawl (CC) web scrape along with smaller, domain-specific datasets. It is expensive to understand the impact of these domain-specific datasets on model capabilities as training at large FLOP scales is required to reveal significant changes to difficult and emergent benchmarks. Given the increasing cost of experimenting with pretraining data, how does one determine the optimal balance between the diversity in general web scrapes and the information density of domain specific data? In this work, we show how to leverage the smaller domain specific datasets by upsampling them relative to CC at the end of training to drive performance improvements on difficult benchmarks. This simple technique allows us to improve up to 6.90 pp on MMLU, 8.26 pp on GSM8K, and 6.17 pp on HumanEval relative to the base data mix for a 7B model trained for 1 trillion (T) tokens, thus rivaling Llama-2 (7B)$\unicode{x2014}$a model trained for twice as long. We experiment with ablating the duration of domain upsampling from 5% to 30% of training and find that 10% to 20% percent is optimal for navigating the tradeoff between general language modeling capabilities and targeted benchmarks. We also use domain upsampling to characterize at scale the utility of individual datasets for improving various benchmarks by removing them during this final phase of training. This tool opens up the ability to experiment with the impact of different pretraining datasets at scale, but at an order of magnitude lower cost compared to full pretraining runs.

Perplexed by Perplexity: Perplexity-Based Data Pruning With Small Reference Models

In this work, we investigate whether small language models can determine high-quality subsets of large-scale text datasets that improve the performance of larger language models. While existing work has shown that pruning based on the perplexity of a larger model can yield high-quality data, we investigate whether smaller models can be used for perplexity-based pruning and how pruning is affected by the domain composition of the data being pruned. We demonstrate that for multiple dataset compositions, perplexity-based pruning of pretraining data can \emph{significantly} improve downstream task performance: pruning based on perplexities computed with a 125 million parameter model improves the average performance on downstream tasks of a 3 billion parameter model by up to 2.04 and achieves up to a $1.45\times$ reduction in pretraining steps to reach commensurate baseline performance. Furthermore, we demonstrate that such perplexity-based data pruning also yields downstream performance gains in the over-trained and data-constrained regimes.

LoRA Learns Less and Forgets Less

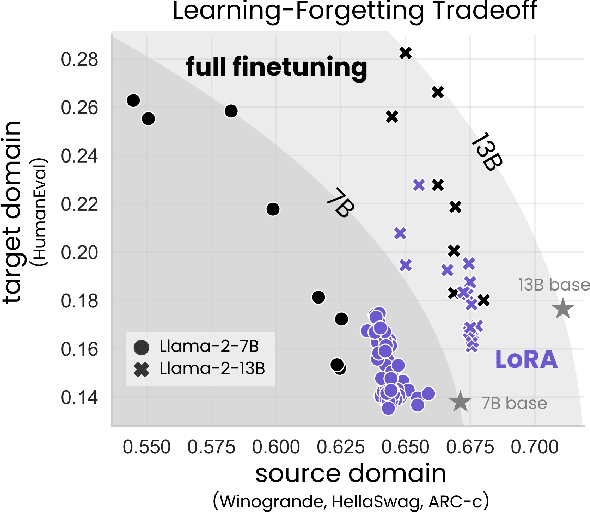
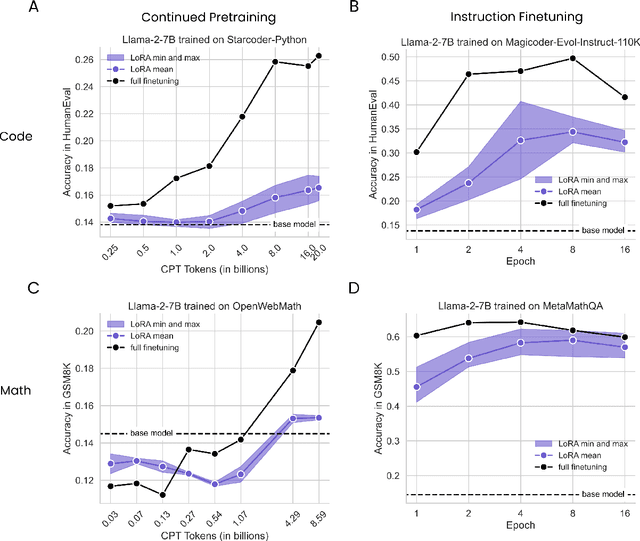
Low-Rank Adaptation (LoRA) is a widely-used parameter-efficient finetuning method for large language models. LoRA saves memory by training only low rank perturbations to selected weight matrices. In this work, we compare the performance of LoRA and full finetuning on two target domains, programming and mathematics. We consider both the instruction finetuning ($\approx$100K prompt-response pairs) and continued pretraining ($\approx$10B unstructured tokens) data regimes. Our results show that, in most settings, LoRA substantially underperforms full finetuning. Nevertheless, LoRA exhibits a desirable form of regularization: it better maintains the base model's performance on tasks outside the target domain. We show that LoRA provides stronger regularization compared to common techniques such as weight decay and dropout; it also helps maintain more diverse generations. We show that full finetuning learns perturbations with a rank that is 10-100X greater than typical LoRA configurations, possibly explaining some of the reported gaps. We conclude by proposing best practices for finetuning with LoRA.

Pretraining task diversity and the emergence of non-Bayesian in-context learning for regression

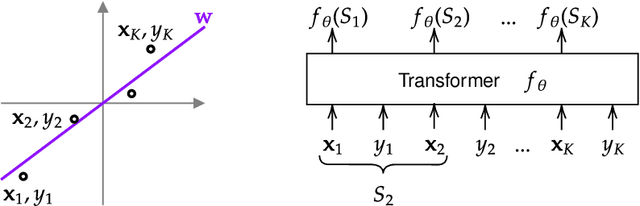
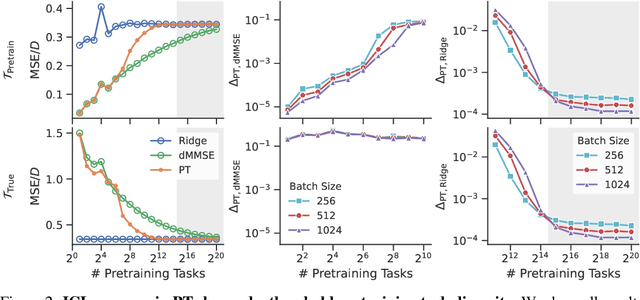
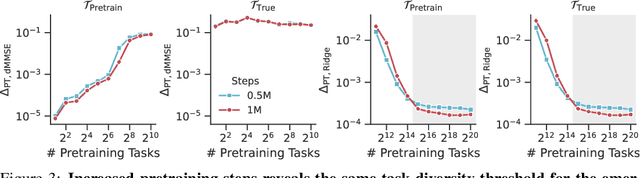
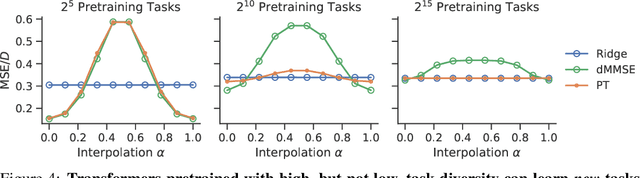
Pretrained transformers exhibit the remarkable ability of in-context learning (ICL): they can learn tasks from just a few examples provided in the prompt without updating any weights. This raises a foundational question: can ICL solve fundamentally $\textit{new}$ tasks that are very different from those seen during pretraining? To probe this question, we examine ICL's performance on linear regression while varying the diversity of tasks in the pretraining dataset. We empirically demonstrate a $\textit{task diversity threshold}$ for the emergence of ICL. Below this threshold, the pretrained transformer cannot solve unseen regression tasks as it behaves like a Bayesian estimator with the $\textit{non-diverse pretraining task distribution}$ as the prior. Beyond this threshold, the transformer significantly outperforms this estimator; its behavior aligns with that of ridge regression, corresponding to a Gaussian prior over $\textit{all tasks}$, including those not seen during pretraining. These results highlight that, when pretrained on data with task diversity greater than the threshold, transformers $\textit{can}$ solve fundamentally new tasks in-context. Importantly, this capability hinges on it deviating from the Bayes optimal estimator with the pretraining distribution as the prior. This study underscores, in a concrete example, the critical role of task diversity, alongside data and model scale, in the emergence of ICL. Code is available at https://github.com/mansheej/icl-task-diversity.

Unmasking the Lottery Ticket Hypothesis: What's Encoded in a Winning Ticket's Mask?

Modern deep learning involves training costly, highly overparameterized networks, thus motivating the search for sparser networks that can still be trained to the same accuracy as the full network (i.e. matching). Iterative magnitude pruning (IMP) is a state of the art algorithm that can find such highly sparse matching subnetworks, known as winning tickets. IMP operates by iterative cycles of training, masking smallest magnitude weights, rewinding back to an early training point, and repeating. Despite its simplicity, the underlying principles for when and how IMP finds winning tickets remain elusive. In particular, what useful information does an IMP mask found at the end of training convey to a rewound network near the beginning of training? How does SGD allow the network to extract this information? And why is iterative pruning needed? We develop answers in terms of the geometry of the error landscape. First, we find that$\unicode{x2014}$at higher sparsities$\unicode{x2014}$pairs of pruned networks at successive pruning iterations are connected by a linear path with zero error barrier if and only if they are matching. This indicates that masks found at the end of training convey the identity of an axial subspace that intersects a desired linearly connected mode of a matching sublevel set. Second, we show SGD can exploit this information due to a strong form of robustness: it can return to this mode despite strong perturbations early in training. Third, we show how the flatness of the error landscape at the end of training determines a limit on the fraction of weights that can be pruned at each iteration of IMP. Finally, we show that the role of retraining in IMP is to find a network with new small weights to prune. Overall, these results make progress toward demystifying the existence of winning tickets by revealing the fundamental role of error landscape geometry.

Lottery Tickets on a Data Diet: Finding Initializations with Sparse Trainable Networks

A striking observation about iterative magnitude pruning (IMP; Frankle et al. 2020) is that $\unicode{x2014}$ after just a few hundred steps of dense training $\unicode{x2014}$ the method can find a sparse sub-network that can be trained to the same accuracy as the dense network. However, the same does not hold at step 0, i.e. random initialization. In this work, we seek to understand how this early phase of pre-training leads to a good initialization for IMP both through the lens of the data distribution and the loss landscape geometry. Empirically we observe that, holding the number of pre-training iterations constant, training on a small fraction of (randomly chosen) data suffices to obtain an equally good initialization for IMP. We additionally observe that by pre-training only on "easy" training data, we can decrease the number of steps necessary to find a good initialization for IMP compared to training on the full dataset or a randomly chosen subset. Finally, we identify novel properties of the loss landscape of dense networks that are predictive of IMP performance, showing in particular that more examples being linearly mode connected in the dense network correlates well with good initializations for IMP. Combined, these results provide new insight into the role played by the early phase training in IMP.

Deep Learning on a Data Diet: Finding Important Examples Early in Training

The recent success of deep learning has partially been driven by training increasingly overparametrized networks on ever larger datasets. It is therefore natural to ask: how much of the data is superfluous, which examples are important for generalization, and how do we find them? In this work, we make the striking observation that, on standard vision benchmarks, the initial loss gradient norm of individual training examples, averaged over several weight initializations, can be used to identify a smaller set of training data that is important for generalization. Furthermore, after only a few epochs of training, the information in gradient norms is reflected in the normed error--L2 distance between the predicted probabilities and one hot labels--which can be used to prune a significant fraction of the dataset without sacrificing test accuracy. Based on this, we propose data pruning methods which use only local information early in training, and connect them to recent work that prunes data by discarding examples that are rarely forgotten over the course of training. Our methods also shed light on how the underlying data distribution shapes the training dynamics: they rank examples based on their importance for generalization, detect noisy examples and identify subspaces of the model's data representation that are relatively stable over training.

Deep learning versus kernel learning: an empirical study of loss landscape geometry and the time evolution of the Neural Tangent Kernel

In suitably initialized wide networks, small learning rates transform deep neural networks (DNNs) into neural tangent kernel (NTK) machines, whose training dynamics is well-approximated by a linear weight expansion of the network at initialization. Standard training, however, diverges from its linearization in ways that are poorly understood. We study the relationship between the training dynamics of nonlinear deep networks, the geometry of the loss landscape, and the time evolution of a data-dependent NTK. We do so through a large-scale phenomenological analysis of training, synthesizing diverse measures characterizing loss landscape geometry and NTK dynamics. In multiple neural architectures and datasets, we find these diverse measures evolve in a highly correlated manner, revealing a universal picture of the deep learning process. In this picture, deep network training exhibits a highly chaotic rapid initial transient that within 2 to 3 epochs determines the final linearly connected basin of low loss containing the end point of training. During this chaotic transient, the NTK changes rapidly, learning useful features from the training data that enables it to outperform the standard initial NTK by a factor of 3 in less than 3 to 4 epochs. After this rapid chaotic transient, the NTK changes at constant velocity, and its performance matches that of full network training in 15% to 45% of training time. Overall, our analysis reveals a striking correlation between a diverse set of metrics over training time, governed by a rapid chaotic to stable transition in the first few epochs, that together poses challenges and opportunities for the development of more accurate theories of deep learning.