Perplexed by Perplexity: Perplexity-Based Data Pruning With Small Reference Models

In this work, we investigate whether small language models can determine high-quality subsets of large-scale text datasets that improve the performance of larger language models. While existing work has shown that pruning based on the perplexity of a larger model can yield high-quality data, we investigate whether smaller models can be used for perplexity-based pruning and how pruning is affected by the domain composition of the data being pruned. We demonstrate that for multiple dataset compositions, perplexity-based pruning of pretraining data can \emph{significantly} improve downstream task performance: pruning based on perplexities computed with a 125 million parameter model improves the average performance on downstream tasks of a 3 billion parameter model by up to 2.04 and achieves up to a $1.45\times$ reduction in pretraining steps to reach commensurate baseline performance. Furthermore, we demonstrate that such perplexity-based data pruning also yields downstream performance gains in the over-trained and data-constrained regimes.

Mini-Batch Optimization of Contrastive Loss

Contrastive learning has gained significant attention as a method for self-supervised learning. The contrastive loss function ensures that embeddings of positive sample pairs (e.g., different samples from the same class or different views of the same object) are similar, while embeddings of negative pairs are dissimilar. Practical constraints such as large memory requirements make it challenging to consider all possible positive and negative pairs, leading to the use of mini-batch optimization. In this paper, we investigate the theoretical aspects of mini-batch optimization in contrastive learning. We show that mini-batch optimization is equivalent to full-batch optimization if and only if all $\binom{N}{B}$ mini-batches are selected, while sub-optimality may arise when examining only a subset. We then demonstrate that utilizing high-loss mini-batches can speed up SGD convergence and propose a spectral clustering-based approach for identifying these high-loss mini-batches. Our experimental results validate our theoretical findings and demonstrate that our proposed algorithm outperforms vanilla SGD in practically relevant settings, providing a better understanding of mini-batch optimization in contrastive learning.

Teaching Arithmetic to Small Transformers

Large language models like GPT-4 exhibit emergent capabilities across general-purpose tasks, such as basic arithmetic, when trained on extensive text data, even though these tasks are not explicitly encoded by the unsupervised, next-token prediction objective. This study investigates how small transformers, trained from random initialization, can efficiently learn arithmetic operations such as addition, multiplication, and elementary functions like square root, using the next-token prediction objective. We first demonstrate that conventional training data is not the most effective for arithmetic learning, and simple formatting changes can significantly improve accuracy. This leads to sharp phase transitions as a function of training data scale, which, in some cases, can be explained through connections to low-rank matrix completion. Building on prior work, we then train on chain-of-thought style data that includes intermediate step results. Even in the complete absence of pretraining, this approach significantly and simultaneously improves accuracy, sample complexity, and convergence speed. We also study the interplay between arithmetic and text data during training and examine the effects of few-shot prompting, pretraining, and model scale. Additionally, we discuss length generalization challenges. Our work highlights the importance of high-quality, instructive data that considers the particular characteristics of the next-word prediction objective for rapidly eliciting arithmetic capabilities.

Dissecting Chain-of-Thought: A Study on Compositional In-Context Learning of MLPs

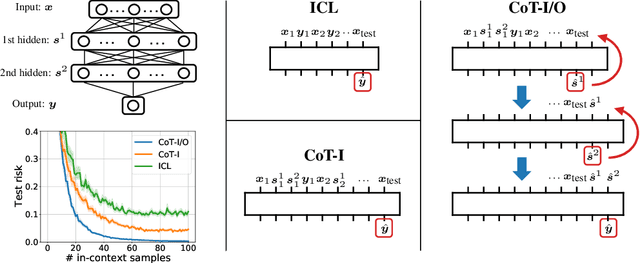
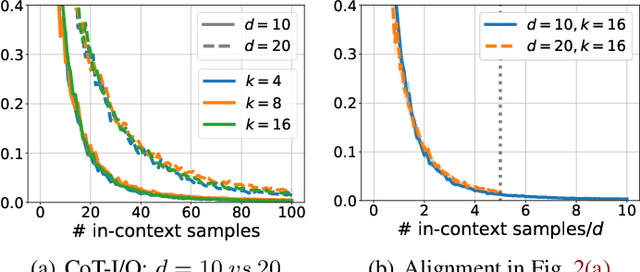
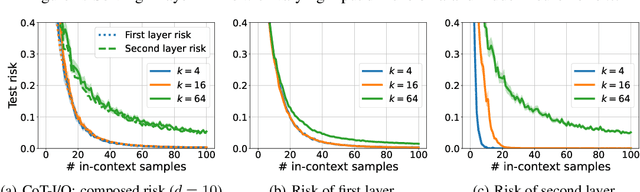
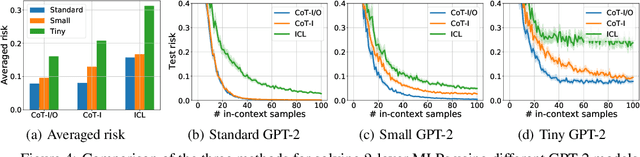
Chain-of-thought (CoT) is a method that enables language models to handle complex reasoning tasks by decomposing them into simpler steps. Despite its success, the underlying mechanics of CoT are not yet fully understood. In an attempt to shed light on this, our study investigates the impact of CoT on the ability of transformers to in-context learn a simple to study, yet general family of compositional functions: multi-layer perceptrons (MLPs). In this setting, we reveal that the success of CoT can be attributed to breaking down in-context learning of a compositional function into two distinct phases: focusing on data related to each step of the composition and in-context learning the single-step composition function. Through both experimental and theoretical evidence, we demonstrate how CoT significantly reduces the sample complexity of in-context learning (ICL) and facilitates the learning of complex functions that non-CoT methods struggle with. Furthermore, we illustrate how transformers can transition from vanilla in-context learning to mastering a compositional function with CoT by simply incorporating an additional layer that performs the necessary filtering for CoT via the attention mechanism. In addition to these test-time benefits, we highlight how CoT accelerates pretraining by learning shortcuts to represent complex functions and how filtering plays an important role in pretraining. These findings collectively provide insights into the mechanics of CoT, inviting further investigation of its role in complex reasoning tasks.

Rare Gems: Finding Lottery Tickets at Initialization

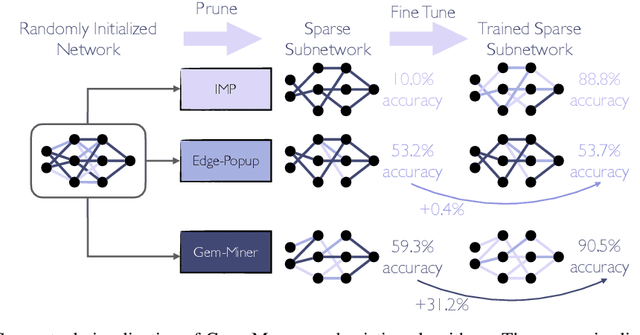
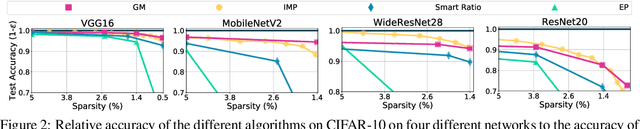
It has been widely observed that large neural networks can be pruned to a small fraction of their original size, with little loss in accuracy, by typically following a time-consuming "train, prune, re-train" approach. Frankle & Carbin (2018) conjecture that we can avoid this by training lottery tickets, i.e., special sparse subnetworks found at initialization, that can be trained to high accuracy. However, a subsequent line of work presents concrete evidence that current algorithms for finding trainable networks at initialization, fail simple baseline comparisons, e.g., against training random sparse subnetworks. Finding lottery tickets that train to better accuracy compared to simple baselines remains an open problem. In this work, we partially resolve this open problem by discovering rare gems: subnetworks at initialization that attain considerable accuracy, even before training. Refining these rare gems - "by means of fine-tuning" - beats current baselines and leads to accuracy competitive or better than magnitude pruning methods.

Finding Everything within Random Binary Networks

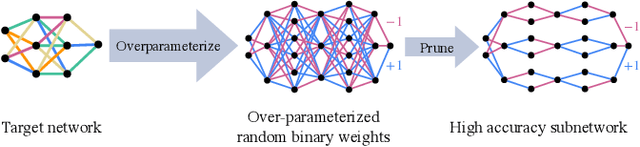
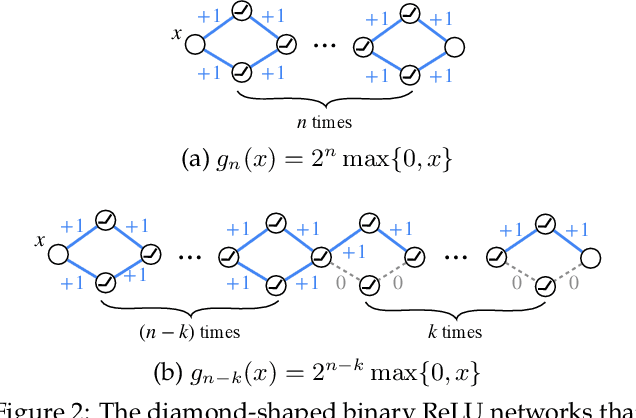
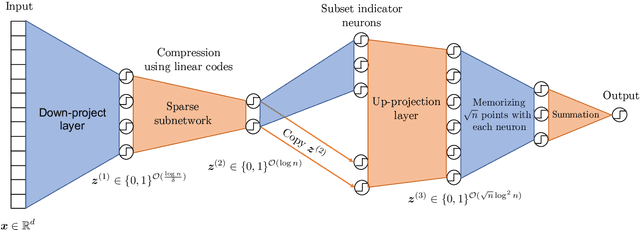
A recent work by Ramanujan et al. (2020) provides significant empirical evidence that sufficiently overparameterized, random neural networks contain untrained subnetworks that achieve state-of-the-art accuracy on several predictive tasks. A follow-up line of theoretical work provides justification of these findings by proving that slightly overparameterized neural networks, with commonly used continuous-valued random initializations can indeed be pruned to approximate any target network. In this work, we show that the amplitude of those random weights does not even matter. We prove that any target network can be approximated up to arbitrary accuracy by simply pruning a random network of binary $\{\pm1\}$ weights that is only a polylogarithmic factor wider and deeper than the target network.

An Exponential Improvement on the Memorization Capacity of Deep Threshold Networks

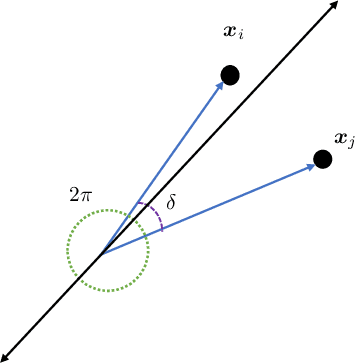
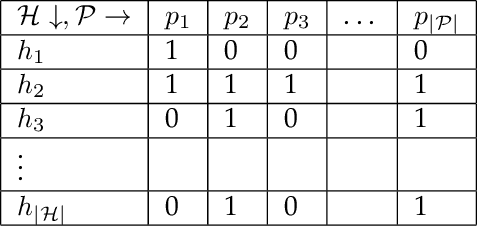
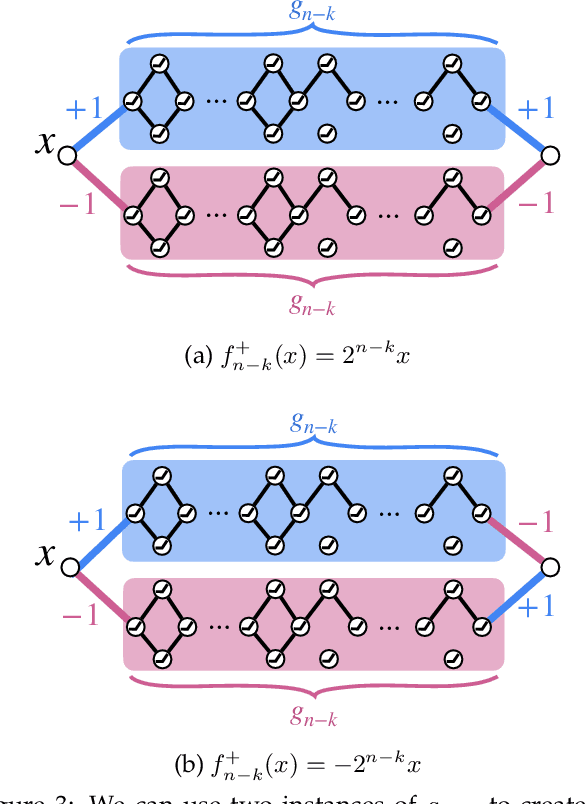
It is well known that modern deep neural networks are powerful enough to memorize datasets even when the labels have been randomized. Recently, Vershynin (2020) settled a long standing question by Baum (1988), proving that \emph{deep threshold} networks can memorize $n$ points in $d$ dimensions using $\widetilde{\mathcal{O}}(e^{1/\delta^2}+\sqrt{n})$ neurons and $\widetilde{\mathcal{O}}(e^{1/\delta^2}(d+\sqrt{n})+n)$ weights, where $\delta$ is the minimum distance between the points. In this work, we improve the dependence on $\delta$ from exponential to almost linear, proving that $\widetilde{\mathcal{O}}(\frac{1}{\delta}+\sqrt{n})$ neurons and $\widetilde{\mathcal{O}}(\frac{d}{\delta}+n)$ weights are sufficient. Our construction uses Gaussian random weights only in the first layer, while all the subsequent layers use binary or integer weights. We also prove new lower bounds by connecting memorization in neural networks to the purely geometric problem of separating $n$ points on a sphere using hyperplanes.

Attack of the Tails: Yes, You Really Can Backdoor Federated Learning

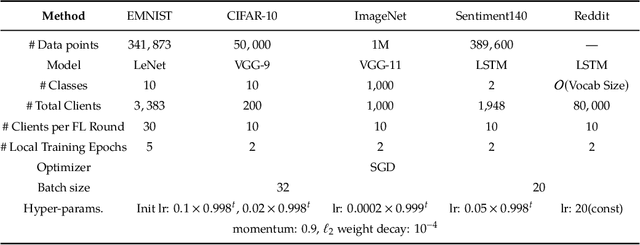
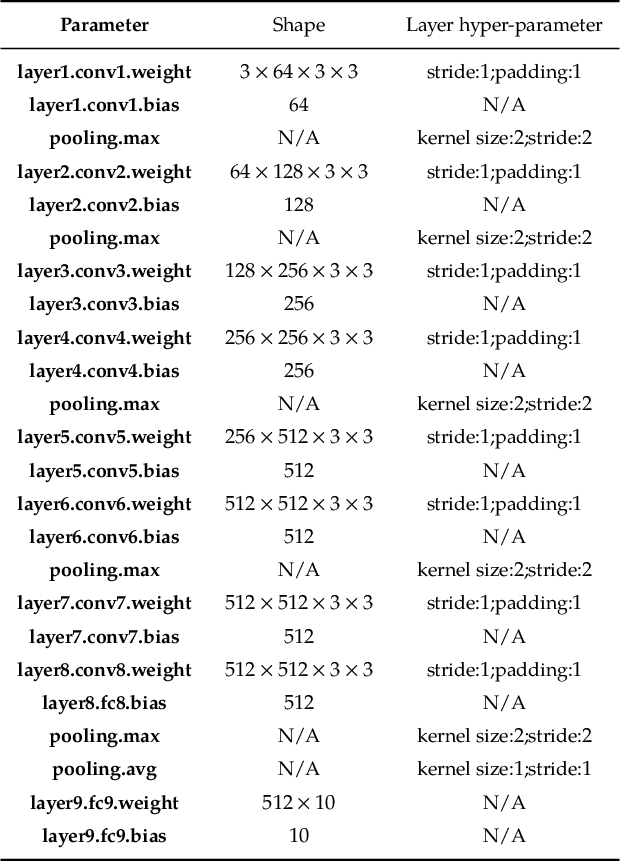
Due to its decentralized nature, Federated Learning (FL) lends itself to adversarial attacks in the form of backdoors during training. The goal of a backdoor is to corrupt the performance of the trained model on specific sub-tasks (e.g., by classifying green cars as frogs). A range of FL backdoor attacks have been introduced in the literature, but also methods to defend against them, and it is currently an open question whether FL systems can be tailored to be robust against backdoors. In this work, we provide evidence to the contrary. We first establish that, in the general case, robustness to backdoors implies model robustness to adversarial examples, a major open problem in itself. Furthermore, detecting the presence of a backdoor in a FL model is unlikely assuming first order oracles or polynomial time. We couple our theoretical results with a new family of backdoor attacks, which we refer to as edge-case backdoors. An edge-case backdoor forces a model to misclassify on seemingly easy inputs that are however unlikely to be part of the training, or test data, i.e., they live on the tail of the input distribution. We explain how these edge-case backdoors can lead to unsavory failures and may have serious repercussions on fairness, and exhibit that with careful tuning at the side of the adversary, one can insert them across a range of machine learning tasks (e.g., image classification, OCR, text prediction, sentiment analysis).