Finding Everything within Random Binary Networks
Paper and Code
Oct 22, 2021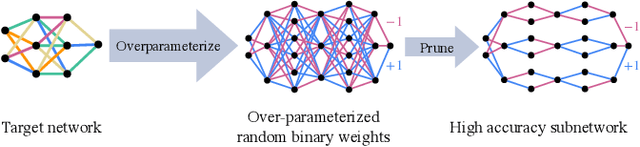

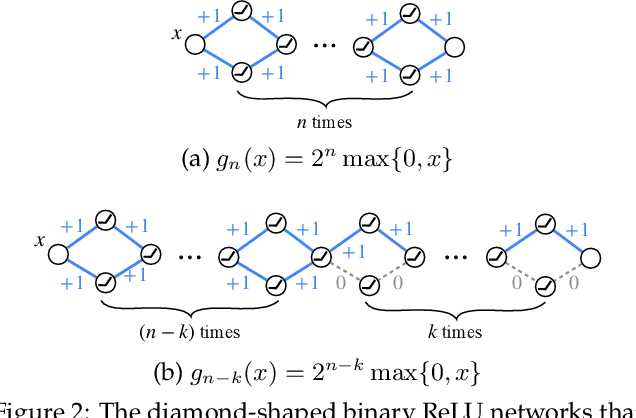
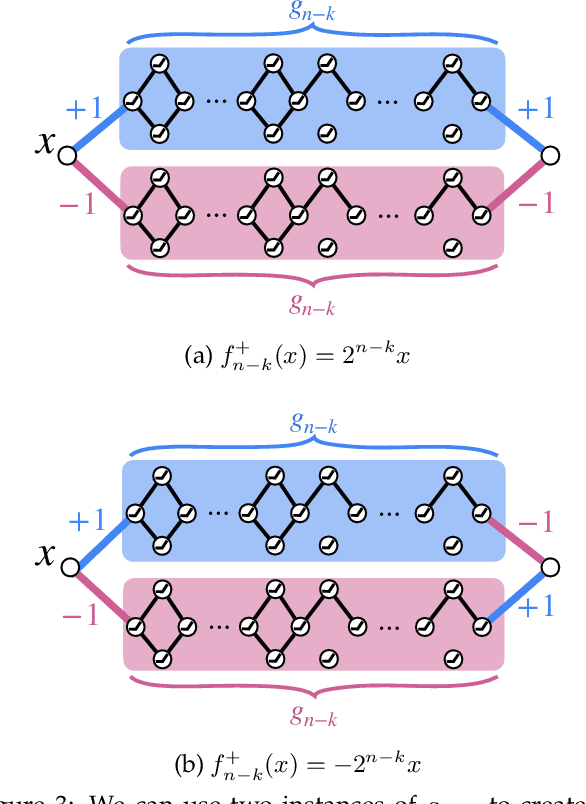
A recent work by Ramanujan et al. (2020) provides significant empirical evidence that sufficiently overparameterized, random neural networks contain untrained subnetworks that achieve state-of-the-art accuracy on several predictive tasks. A follow-up line of theoretical work provides justification of these findings by proving that slightly overparameterized neural networks, with commonly used continuous-valued random initializations can indeed be pruned to approximate any target network. In this work, we show that the amplitude of those random weights does not even matter. We prove that any target network can be approximated up to arbitrary accuracy by simply pruning a random network of binary $\{\pm1\}$ weights that is only a polylogarithmic factor wider and deeper than the target network.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge