Scalable Anomaly Detection in Large Homogenous Populations
Paper and Code
Sep 20, 2013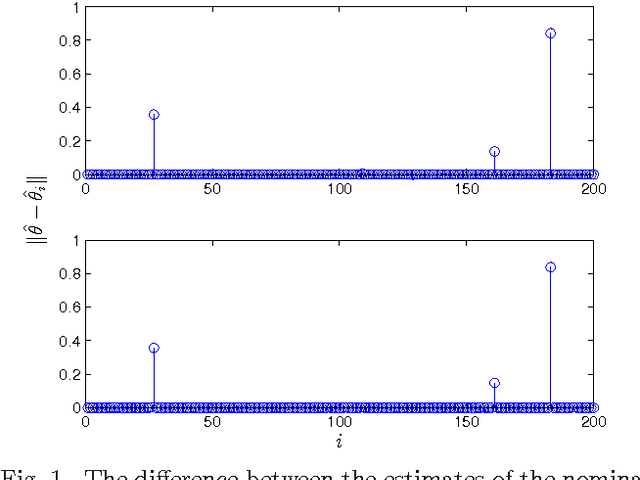
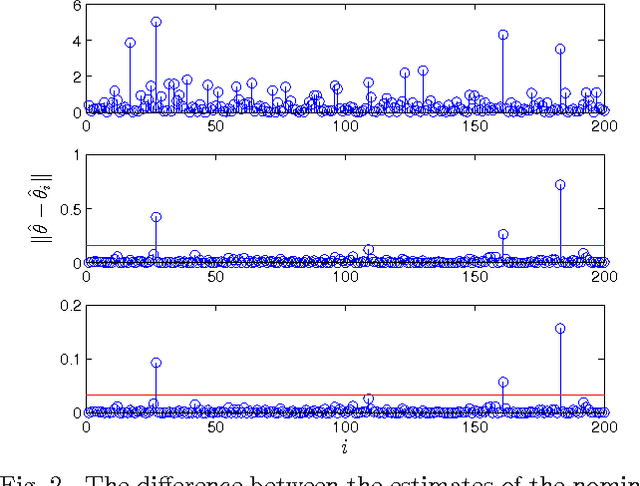
Anomaly detection in large populations is a challenging but highly relevant problem. The problem is essentially a multi-hypothesis problem, with a hypothesis for every division of the systems into normal and anomal systems. The number of hypothesis grows rapidly with the number of systems and approximate solutions become a necessity for any problems of practical interests. In the current paper we take an optimization approach to this multi-hypothesis problem. We first observe that the problem is equivalent to a non-convex combinatorial optimization problem. We then relax the problem to a convex problem that can be solved distributively on the systems and that stays computationally tractable as the number of systems increase. An interesting property of the proposed method is that it can under certain conditions be shown to give exactly the same result as the combinatorial multi-hypothesis problem and the relaxation is hence tight.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge