On the Geometry of Message Passing Algorithms for Gaussian Reciprocal Processes
Paper and Code
Apr 06, 2016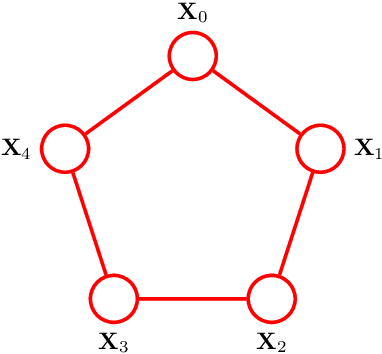
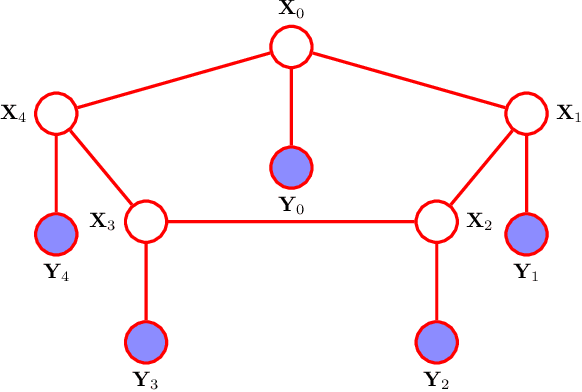
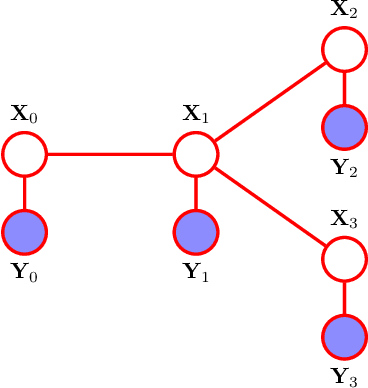
Reciprocal processes are acausal generalizations of Markov processes introduced by Bernstein in 1932. In the literature, a significant amount of attention has been focused on developing dynamical models for reciprocal processes. Recently, probabilistic graphical models for reciprocal processes have been provided. This opens the way to the application of efficient inference algorithms in the machine learning literature to solve the smoothing problem for reciprocal processes. Such algorithms are known to converge if the underlying graph is a tree. This is not the case for a reciprocal process, whose associated graphical model is a single loop network. The contribution of this paper is twofold. First, we introduce belief propagation for Gaussian reciprocal processes. Second, we establish a link between convergence analysis of belief propagation for Gaussian reciprocal processes and stability theory for differentially positive systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge